Üslü İfadelerle İlgili Temel Kurallar Konu Anlatımı

Kazanım: Üslü ifadelerle ilgili temel kuralları anlar, birbirine denk ifadeler oluşturur.

Üslü İfadelerle ilgili temel kurallar konu anlatımı üslü sayılarda işlem yaparken kullanacağımız temel becerileri kapsayan yöntemlerdir.

Üslü İfadelerde Çarpma İşlemi

Üslü ifadelerde çarpma işlemi yaparken tabanların aynı olması kuralı ve üslerin aynı olması kuralı olmak üzere 2 kural öğreneceğiz. Üslü ifadelerde hızlı hesaplama yapmak isterseniz, hesaptablosu.net/uslu-sayi-hesaplama-makinesi/ sayfasından pratik üslü sayı hesaplamaları yapabilirsiniz.

Bilgi: Üslü ifadelerde çarpma işlemi yapılırken;

✅ Tabanlar ayını ise üsler toplanır. aⁿ×a^m = a^n+m

✅ Üsleri aynı tabanları farklı ise tabanlar çarpılır. aⁿ×bⁿ = (a×b)ⁿ

Örnek: Aşağıda verilen üslü ifadelerdeki çarpma işlemlerini yapıp sonucu üslü olarak bulalım.

✅ 2⁴×2⁵ = ?

➡ Tabanlar ayını ise üsler toplanır.

➡ 2⁴×2⁵ = 2⁴⁺⁵ = 2⁹

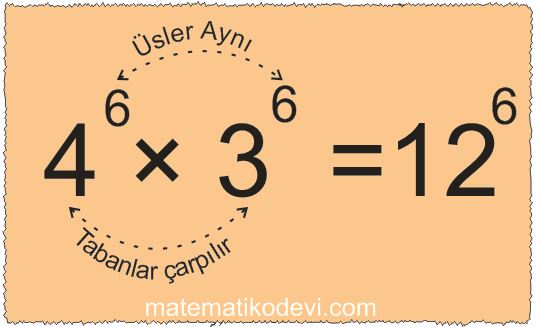
✅ 3⁷×5⁷ = ?

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır.

➡ 3⁷×5⁷ = (3×5)⁷ = 15⁷

✅ 4⁷×4⁶ = ?

➡ Tabanlar ayını ise üsler toplanır.

➡ 4⁷×4⁶ = 4⁷⁺⁶ = 4¹³

✅ 9⁸×5⁸ = ?

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır.

➡ 9⁸×5⁸ = (9×5)⁷ = 45⁷

✅ 7⁵×7^-4×7⁶= ?

➡ Tabanlar ayını ise üsler toplanır.

➡ 7⁵×7^-4×7⁶= 7^5+(-4)+6 = 7⁷

✅ 3⁵×(-4)⁵×2⁵= ?

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır.

➡ 3⁵×(-4)⁵×2⁵ = (3×(-4)×2)⁵ = (-24)⁵

Üssün Üssü (Kuvvetin Kuvveti)

Bilgi: (a^b)^c şeklinde yazımlara üssün üssü denir. Üssün üssü olan durumlarda üsler çarpılır. a^b×c

✅ Üs art arda kaç tane olursa olsun üslerin hepsi çarpılır. Örneğin; ((3²)³)⁴ = 3²⁴

Örnek: Aşağıda verilen üssün üssü ifadelerine eşit olan üslü ifadeleri bulalım.

✅ (6²)³ =?

➡ Üssün üssü olan durumlarda üsler çarpılır.

(6²)³ = 6^2×3 = 6⁶

✅ (9^-5)⁴ =?

➡ Üssün üssü olan durumlarda üsler çarpılır.

(9^-5)⁴ = 9^(-5)×4 = 9^-20

✅ (8^-3)^-7 =?

➡ Üssün üssü olan durumlarda üsler çarpılır.

(8^-3)^-7 = (8^(-3)×(-7) = 8²¹

Not: Bir üslü ifadede tabandaki sayı bir sayının üslü ifadesi olarak yazılabiliyorsa bu üslü ifadeyi üssün üssü olarak yazabiliriz.

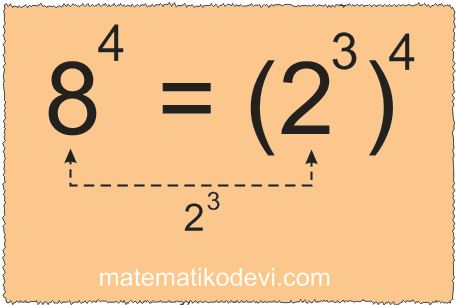
Örnek:Aşağıda verilen üslü ifadeleri istenen tabana göre çevirelim.

✅ 125⁴ =?

➡ Tabandaki 125 sayısı 5’in kuvveti şeklinde yazılabilir.

➡ 125=5³

➡ 125⁴ = (5³ )⁴=5¹²

✅ 27^-6 =?

➡ Tabandaki 27 sayısı 3’ün kuvveti şeklinde yazılabilir.

➡ 27=3³

➡ 27^-6 = (3³ )^-6=3^-18

✅ 32^-7 =?

➡ Tabandaki 32 sayısı 2’nin kuvveti şeklinde yazılabilir.

➡ 32=2⁵

➡ 32^-7 = (2⁵ )^-7=2^-35

Not: Üssün üssü durumlarında işaret tespiti yaparken parantez dışındaki üsse dikkat etmeliyiz.

Örneğin; Aşağıdaki örneklerde parantez dışındaki üs çift olduğunda sonuç pozitif , üs tek olduğunda sonuç negatif olduğunu görürüz.

✅ Taban negatif parantez dışındaki üs çift olursa sonuç pozitif olur. (-3³ )⁸= pozitif

✅ Taban negatif parantez dışındaki üs tek olursa sonuç negatif olur. (-5⁴ )⁷= negatif

✅ Taban pozitif parantez olursa sonuç her zaman pozitif olur. (7⁴)⁸= pozitif

Örnek: Aşağıda verilen üssün üssü durumlarındaki sayıların işaretini bulalım.

✅ (-5⁴ )⁷ = ?

➡ (-5⁴ )⁷ taban negatif parantez dışındaki üs tek olduğu için sonuç negatif

➡ (-5⁴ )⁷ = negatif

✅ (-6³ )⁴ = ?

➡ (-6³ )⁴ taban negatif parantez dışındaki üs çift olduğu için sonuç pozitif

➡ (-5⁴ )⁷ = pozitif

✅ (-5⁴ )⁷ = ?

➡ (-5⁴ )⁷ taban negatif parantez dışındaki üs tek olduğu için sonuç negatif

➡ (-5⁴ )⁷ = negatif

Not: Üssün üssü kuralını kullanarak karşılaştırma sorularını çözebiliriz.

Örnek: Aşağıda verilen noktalı yerlere ”>,<” sembollerini uygun olacak şekilde yazalım.

✅ 16⁵ ….8⁷

➡ 16=2⁴

➡ 16⁵ = (2⁴ )⁵=2²⁰

➡ 8=2³

➡ 8⁷ = (2³ )⁷=2²¹

➡ 2²⁰ ifadesi 2²¹ ifadesinden küçüktür.

➡ 16⁵ ifadesi 8⁷ ifadesinden küçüktür. (16⁵<8⁷)

Not: Üslü ifadelerin eşitliğinde üsde bilinmeyen varsa önce tabanları eşitleriz sonra üsleri bir birbirine eşitleriz.

Üslü ifadede bilinmeyeni bulmak için aşağıdaki adımları takip ederiz.

✅ Bilinmeyeni bulmak için tabanların eşit olması lazım

✅ Üssün üssü kuralına göre tabanları eşitleriz.

✅ Tabanlar eşitlendikten sonra üsler birbirine eşitlenir.

✅ Üsleri eşitledikten sonra 7.sınıfda öğrendiğimiz denklem çözme metoduna göre bilinmeyeni buluruz.

Örnek: 2^2x = 8⁶ üslü ifade eşitliğinde bilinmeyeni bulalım.

✅ Bilinmeyeni bulmak için tabanların eşit olması lazım

➡ 2^2x = 8⁶

✅ Üssün üssü kuralına göre tabanları eşitleriz.

➡ 2^2x = (2³)⁶ ❗ (8 = 2³) 🤓

➡2^2x = 2¹⁸

✅ Tabanlar eşitlendikten sonra üsler birbirine eşitlenir.

➡ 2x = 18

✅ Üsleri eşitledikten sonra denklem çözme metoduna göre bilinmeyeni buluruz.

➡ 2x = 18 ❗ (her iki tarafı ikiye böleriz.) 🤓

➡ x = 9 ❗

Örnek: 9^x-1 = 27¹² üslü ifade eşitliğinde bilinmeyeni bulalım.

✅ Bilinmeyeni bulmak için tabanların eşit olması lazım

➡ 9^x-1 = 27¹²

✅ Üssün üssü kuralına göre tabanları eşitleriz.

➡ (3²)^x-1 = (3³)¹²

➡ 3^2x-2 = 3³⁶

✅ Tabanlar eşitlendikten sonra üsler birbirine eşitlenir.

➡ 2x-2=36

✅ Üsleri eşitledikten sonra denklem çözme metoduna göre bilinmeyeni buluruz.

➡ 2x-2=36 ❗ (-2’yi eşitliğin diğer tarafına atarız.) 🤓

➡ 2x=38 ❗ ( her iki tarafı 2’ye böleriz) 🤓

➡ x=19

Bilgi: Üslü ifadeleri parçalarken(iki üslü ifadenin çarpımı şeklinde yazarken ) çarpma işleminin 2 kuralını kullanırız.

Örneğin;

✅ Tabanlar ayını ise üsler toplanır kuralına göre 2¹⁴ ifadesini 2¹⁰×2⁴ şeklinde parçalayabiliriz.

✅ Üsleri aynı tabanları farklı ise tabanlar çarpılır kuralına göre 6¹⁰ ifadesini 3¹⁰×2¹⁰ şeklinde parçalayabiliriz.

Örnek: Aşağıdaki üslü ifadelerin çarpma işleminin kuralından yararlanarak parçalanmış hallerini bulalım.

✅ 10⁶

➡ Tabanlar ayını ise üsler toplanır kuralına göre 10⁵×10¹ veya 10⁴×10² şeklinde yazılabilir.

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır kuralına göre 5⁶×2⁶ şeklinde yazılır.

✅ 12⁴

➡ Tabanlar ayını ise üsler toplanır kuralına göre 12³×12¹ veya 12²×12² şeklinde yazılabilir.

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır kuralına göre 4⁴×3⁴ veya 2⁴×6⁴ şeklinde yazılabilir.

✅ 9⁷

➡ Tabanlar ayını ise üsler toplanır kuralına göre 9⁶×9¹ , 9⁵×9² , 9⁴×9³ şeklinde yazılabilir.

➡ Üsleri aynı tabanları farklı ise tabanlar çarpılır kuralına göre 3⁷×3⁷ şeklinde yazılır.

Bilgi: Üslü olarak verilen ifadenin kaç basamaklı olduğunu bulmak için verilen üslü ifadeyi 10 ‘un kuvveti şeklinde yazarız.

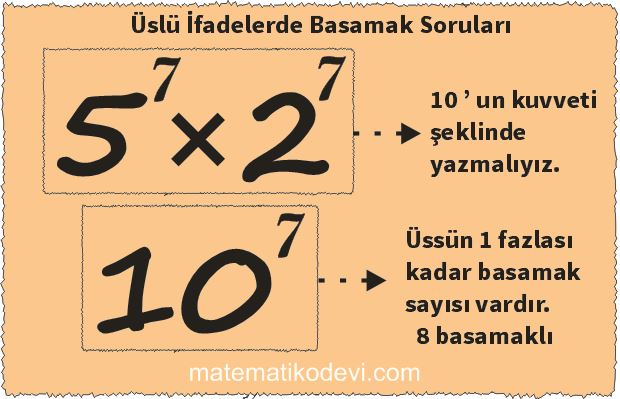
Örnek: Aşağıda verilen üslü ifadelerin kaç basamaklı olduğunu bulalım.

✅ 2⁸×5⁸

➡ 10 ‘ un kuvveti şeklinde yazmalıyız.

2⁸×5⁸ = 10⁸

➡ Üssün 1 fazlası kadar basamak sayısı vardır.

10⁸ 👉 8+1 =9 basamaklı

✅ 2¹¹×5¹¹

➡ 10 ‘ un kuvveti şeklinde yazmalıyız.

2¹¹×5¹¹ = 10¹¹

➡ Üssün 1 fazlası kadar basamak sayısı vardır.

10¹¹ 👉 11+1 =12 basamaklı

Not: Basamak sorularında çarpım durumundaki katsayının basamak sayısı ile 10 ‘un kuvveti şeklindeki üssün toplamı basamak sayısını verir.

Örneğin; 127 × 10¹⁵ ifadesinin kaç basamaklı olduğunu aşağıdaki gibi buluruz.

✅ 127 × 10¹⁵ = 3 +15 = 18 basamaklı

Örnek: Aşağıda verilen üslü ifadelerin kaç basamaklı olduğunu bulalım.

✅ 7 × 10⁶

➡ 7 × 10⁶ (1+6=7 basamaklı)

✅ 15 × 10⁹

➡ 15 × 10⁹ (2+9=11 basamaklı)

✅ 184 × 10¹³

➡ 184 × 10¹³ (3+13=16 basamaklı)

✅ 1453× 10¹⁸

➡ 1453 × 10¹⁸ (4+18=22 basamaklı)

Not: Basamak sorularında üsler aynı değil ise üsler aynı olacak şekilde parçalarız.

Örneğin; 2⁹×5⁷ ifadesinin kaç basamaklı olduğunu bulmak için üsleri aynı yapmalıyız. 2⁹ ifadesini 2²×2⁷ şeklinde yazarsak 5⁷ ifadesi ile aynı üs olur.

✅ 2⁹×5⁷ = 2²×2⁷×5⁷

Sonra 2²×2⁷×5⁷ ifadesinde 2⁷×5⁷ ifadesinin üsleri aynı olduğu için tabanları çarpılır. 👉 2⁷×5⁷ = 10⁷

2²×2⁷×5⁷ ifadesini 2²×10⁷ olarak yazarız.

Katsayı olan 2² sonucunu yazarız. 👉2²×10⁷ = 4×10⁷

2⁹×5⁷ ifadesi 4×10⁷ ifadesine dönüşür.

Şimdi 4×10⁷ ifadesinin kaç basamaklı olduğunu bulabiliriz.

4×10⁷ = 1+7 = 8 basamaklı

Örnek: Aşağıda verilen üslü ifadelerin kaç basamaklı olduğunu bulalım.

✅ 2¹³×5¹⁰

➡ Üsler aynı olacak şekilde parçalarız.

2³×2¹⁰×5¹⁰ ❗ (2¹³ = 2³×2¹⁰) 🤓

2³ × 10¹⁰ ❗ (2¹⁰×5¹⁰ = 10¹⁰) 🤓

8 × 10¹⁰ ❗ (1+10=11 basamaklı) 🤓

✅ 2¹²×5¹⁵

➡ Üsler aynı olacak şekilde parçalarız.

2¹²×5¹²×5³ ❗ (5¹⁵ = 5¹²×5³) 🤓

5³ × 10¹² ❗ (2¹²×5¹² = 10¹²) 🤓

125× 10¹² ❗ (3+12=15 basamaklı) 🤓

Üslü İfadelerde Bölme İşlemi

Üslü ifadelerde bölme işlemi yaparken tabanların aynı olması kuralı ve üslerin aynı olması kuralı olmak üzere 2 kural öğreneceğiz.

Bilgi: Tabanları aynı olan üslü sayılarla bölme işlemi yapılırken payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

✅ \dfrac{a^x}{a^y} = a^x-y

Örneğin aşağıdaki görseli incelediğimizde sonucun 4² çıktığını görürüz. Bunu pratik olarak 4^5-3= 4² şeklinde buluruz.

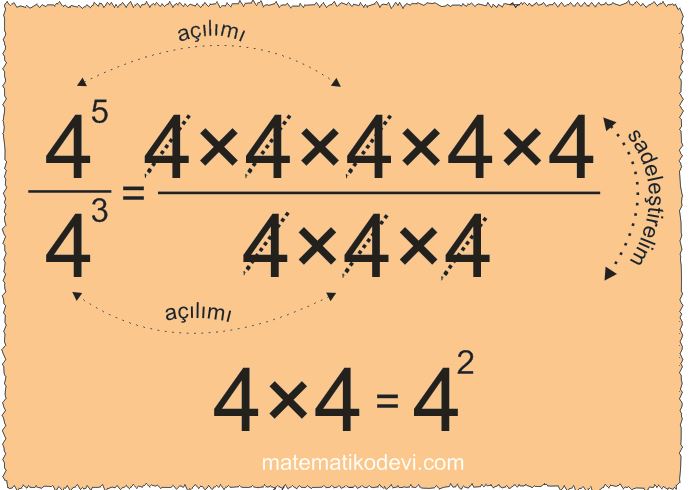
Örnek: Aşağıdaki üslü ifadelerle ilgili bölme işlemlerini yapalım.

✅ \dfrac{5^8}{5^6} = ?

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

5^8-6

5²

✅ \dfrac{7^{11}}{ 7^8} = ?

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

7^11-8

7³

✅ \dfrac{9^6}{9^ {13}} = ?

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

9^6-13

9^-7

✅ \dfrac{3^ {-5}}{3^ {-12}} = ?

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

3^(-5)-(-12)

❗ (hem çıkartmadan dolayı eksi var hemde paydadaki sayı eksi var iki eksi ard arda geliyor. ) 🤓

3^-5+12

❗ (eksi ile eksinin çarpımı artıya dönüşür.) 🤓

3⁷

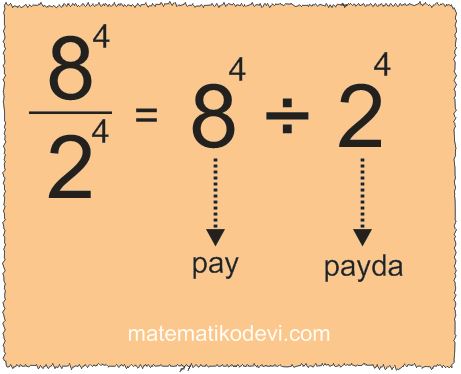
Bilgi: Üslü ifadelerde bölme işlemi yapılırken üsler aynı ise tabanlar bölünür , üsler aynen yazılır.

✅ \dfrac{a^x}{b^x} = ( \dfrac{a}{b}) ^x

Örneğin; Aşağıdaki görselde sonucun 4⁴ çıktığını görürüz. Bunu pratik olarak (8÷2)⁴ = 4⁴ şeklinde buluruz.

Örnek: Aşağıdaki üslü ifadelerle ilgili bölme işlemlerini yapalım.

✅ \dfrac{10^3}{5^3} = ?

➡ Üsler aynı ise tabanlar bölünür , üsler aynen yazılır.

( \dfrac{10}{5}) ³

2³

✅ \dfrac{-12^5}{4^5} = ?

➡ Üsler aynı ise tabanlar bölünür , üsler aynen yazılır.

( \dfrac{-12}{4}) ⁵ ❗ (Bölme işlemi yaparken işaretleri unutma.) 🤓

(-3)⁵

✅ \dfrac{-8^6}{-4^6} = ?

➡ Üsler aynı ise tabanlar bölünür , üsler aynen yazılır.

( \dfrac{-8}{-4}) ⁶ ❗ (Bölme işlemi yaparken işaretleri unutma.) 🤓

2⁶

Not: Üslü ifadelerde bölme işleminde üsler ve tabanlar aynı değilse üssün üssü kuralını kullanarak üsleri veya tabanları aynı yapmaya çalışırız.

Örnek: Aşağıdaki üslü ifadelerle ilgili bölme işlemlerini yapalım.

✅ \dfrac{10^8}{25^4} = ?

➡ Yukarıdaki bölme işleminde hem üsler hemde tabanlar aynı değil bu durumda üssün üssü kuralına göre üsleri veya tabanları aynı yapmaya çalışalım.

25⁴ = (5²)⁴ = 5⁸ ❗ (25⁴ yerine 5⁸ yazalım) 🤓

\dfrac{10^8}{5^8} ❗ (üsleri aynı oldu) 🤓

➡ Üsler aynı ise tabanlar bölünür , üsler aynen yazılır.

( \dfrac{10}{5}) ³

2⁸

✅ \dfrac{16^7}{8^5} = ?

➡ Yukarıdaki bölme işleminde hem üsler hemde tabanlar aynı değil bu durumda üssün üssü kuralına göre üsleri veya tabanları aynı yapmaya çalışalım.

16⁷ = (2⁴)⁷ = 2²⁸ ❗ (16⁷ yerine 2²⁸ yazalım) 🤓

8⁵ = (2³)⁵ = 2¹⁵ ❗ (8⁵ yerine 2¹⁵ yazalım) 🤓

2²⁸ / 2¹⁵ ❗ (tabanları aynı oldu) 🤓

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

2^28-15

2¹³

✅ \dfrac{9^6}{27^5} = ?

➡ Yukarıdaki bölme işleminde hem üsler hemde tabanlar aynı değil bu durumda üssün üssü kuralına göre üsleri veya tabanları aynı yapmaya çalışalım.

9⁶ = (3²)⁶ = 3¹² ❗ (9⁶ yerine 3¹² yazalım) 🤓

27⁵ = (3³)⁵ = 3¹⁵ ❗ (27⁵ yerine 3¹⁵ yazalım) 🤓

3¹² / 3¹⁵ ❗ (tabanları aynı oldu) 🤓

➡ Tabanlar aynı ise payın üssünden paydanın üssü çıkartılır, taban aynen yazılır.

3^12-15

3^-3

🎥 Bir Soru Bir Video 🎥

Soru:

Bilgi: a≠0 ve x,y birer tam sayı olamak üzere ;

(a^x)^y = a^x·y ve \dfrac{a^x}{a^y} = a^x-y

Aşağıda verilen eşit kollu teraziler dengededir.

Yukarıda verilen eşit kollu terazinin sol kefesinde bulunan cismin kütlesi 16⁵ miligramdır.

Yukarıda verilen eşit kollu terazinin sol kefesinde bulunan cismin bir tanesinin kütlesi 8⁷ miligramdır.

Buna göre cisminin kütlesi cismin kütlesinin kaç katıdır?

A) 32

B) 8

C) \dfrac{1}{4}

D) \dfrac{1}{32}

Çözüm: