Rasyonel Sayılarla Toplama ve Çıkarma İşlemi
Kazanım: Rasyonel sayılarla toplama ve çıkarma işlemlerini yapar.
Bu konuda neler öğreneceğiz :
Rasyonel Sayılarla Toplama ve Çıkarma İşlemi
Rasyonel Sayılarla Toplama İşlemi
Rasyonel sayılarla toplama işlemi yapılırken rasyonel sayıların paydalarına bakarız.
- Rasyonel sayıların paydaları eşit ise paylar toplanır ve payda aynen yazılır.
Örneğin;
\dfrac{5}{7} + ( \dfrac{-8}{5} ) =
\dfrac{5+(-8)}{5} =
\dfrac{-3}{10}
Paydaları eşit olmayan rasyonel sayılarla toplama işlemi yapılırken;
- Paydalar eşitlenir.
- Paylar toplanır.
- Payda aynen yazılır.
Örneğin;
\dfrac{4}{9} + ( \dfrac{-5}{6} ) =
\dfrac{4×2}{9×2} + ( \dfrac{-5×3}{6×3} ) =
\dfrac{8}{18} + ( \dfrac{-15}{18} ) =
\dfrac{8+(-15)}{18} =
\dfrac{-7}{18}
Rasyonel Sayılarla Çıkarma İşlemi
Rasyonel sayılarla çıkarma işlemi yapılırken rasyonel sayıların paydalarına bakarız.
- Rasyonel sayıların paydaları eşit ise paylar çıkarılır ve payda aynen yazılır.
Örneğin;
\dfrac{3}{8} – \dfrac{7}{8} =
\dfrac{3 - 7}{8} =
\dfrac{-4}{8}
Paydaları eşit olmayan rasyonel sayılarla çıkarma işlemi yapılırken ;
- Rasyonel sayıların paydaları eşitlenir.
- Paylar çıkarılır.
- Payda aynen yazılır.
Örneğin;
\dfrac{3}{4} – \dfrac{2}{3} =
\dfrac{3×3}{4×3} – \dfrac{2×4}{3×4} =
\dfrac{9}{12} – \dfrac{8}{12} =
\dfrac{9-8}{12} =
\dfrac{1}{12}
Rasyonel Sayılarla Toplama İşleminin Özellikleri
Rasyonel sayılarla toplama işlemi yapılırken toplanan sayıların yerlerinin değişmesi toplama işleminin sonucunu değiştirmez. Bu duruma ” rasyonel sayılarda toplama işleminin değişme özelliği vardır.” denir.
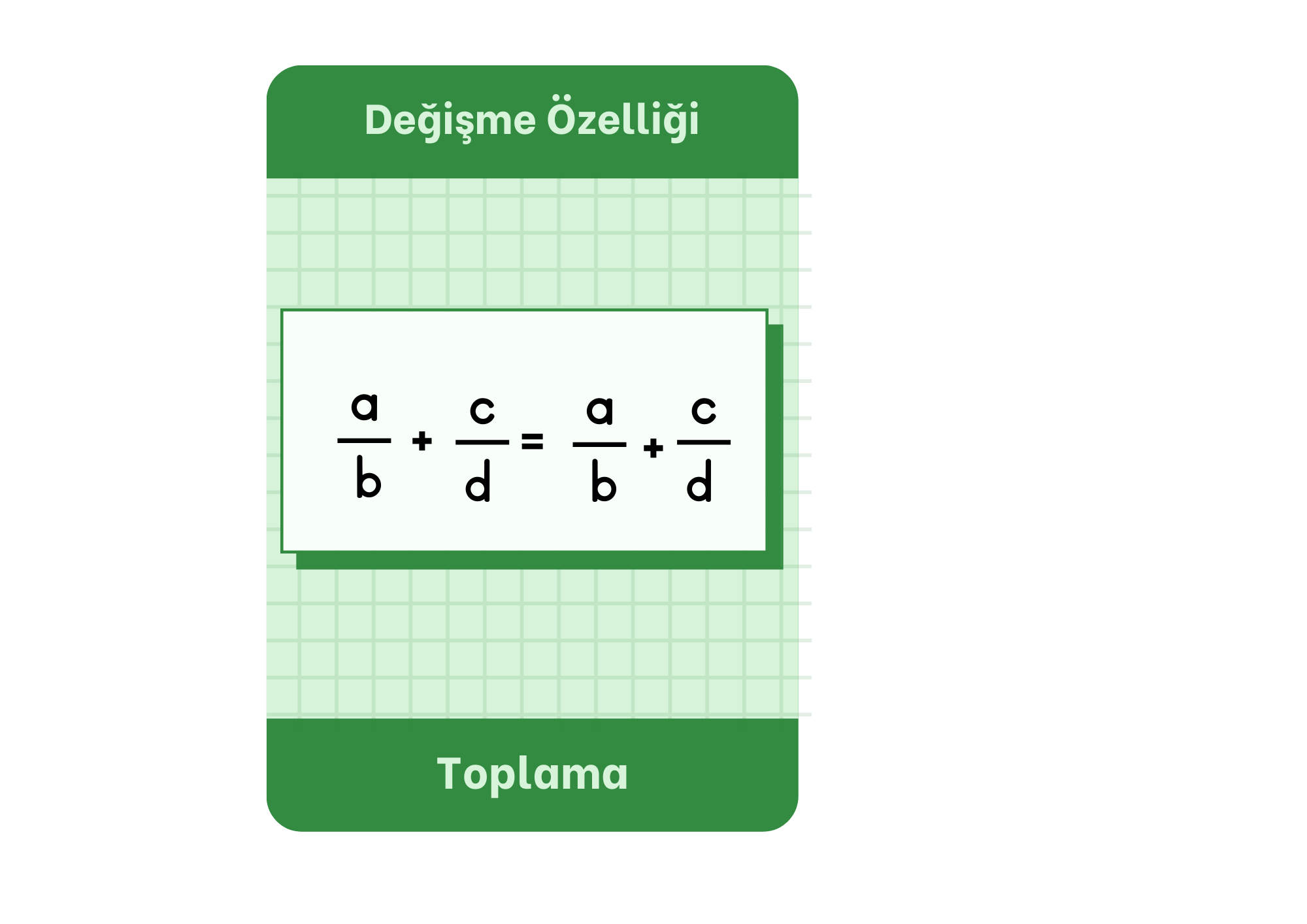
Örneğin;
\dfrac{3}{4} + \dfrac{2}{5} = \dfrac{2}{5} + \dfrac{3}{4}
\dfrac{3×5}{4×5} + \dfrac{2×4}{5×4} = \dfrac{2×4}{5×4} + \dfrac{3×5}{4×5}
\dfrac{15}{20} + \dfrac{8}{20} = \dfrac{8}{20} + \dfrac{15}{20}
\dfrac{23}{20} = \dfrac{23}{20}
🤓 Yukarıda görüldüğü gibi rasyonel sayıların yerini değiştirdiğimizde sonuç aynı çıkıyor. O zaman arkadaşlar rasyonel sayılarda toplama işlemi yaparken sayıların yerini değiştirdiğimizde sonuç değişmez.
Rasyonel sayılarda toplama işleminin etkisiz elemanı 0‘dır. Yani bir rasyonel sayıyı sıfır ile toplarsak sonuç yine aynı rasyonel sayı olur.

Örneğin;
\dfrac{5}{12} + 0 = \dfrac{5}{12}
0 + \dfrac{5}{12} = \dfrac{5}{12}
Not: Rasyonel sayılarda çıkarma işleminde etkisiz eleman sıfır değildir.
\dfrac{a}{b} bir rasyonel sayısı ile toplandığında etkisiz elemanı (sıfır) veren sayıya bu sayının toplama işlemine göre tersi denir.
- \dfrac{a}{b} rasyonel sayısının toplama işlemine göre tersi – \dfrac{a}{b} ‘dır.

Örneğin;
\dfrac{2}{5} rasyonel sayısının toplama işlemine göre tersi ➡️ – \dfrac{2}{5}
– \dfrac{4}{7} rasyonel sayısının toplama işlemine göre tersi ➡️ \dfrac{4}{7}
\dfrac{4}{9} rasyonel sayısının toplama işlemine göre tersi ➡️ – \dfrac{4}{9}
Üç veya daha fazla rasyonel sayı ile toplama işlemi yaparken, toplama işlemine önce istediğimiz iki sayıdan başlayabiliriz. Rasyonel sayılarla toplama işleminin bu özelliğine birleşme özelliği denir.

Örneğin;
( \dfrac{3}{10} + \dfrac{9}{10} ) + \dfrac{7}{10} = \dfrac{3}{10} + ( \dfrac{9}{10} + \dfrac{7}{10} )
\dfrac{12}{10} + \dfrac{7}{10} = \dfrac{3}{10} + \dfrac{16}{10}
\dfrac{19}{10} = \dfrac{19}{10}
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Rasyonel Sayılarla Çarpma ve Bölme İşlemi |

