Rasyonel Sayılarla Çok Adımlı İşlemler
Kazanım: Rasyonel sayılarla çok adımlı işlemleri yapar.
Bu konuda neler öğreneceğiz :
Rasyonel Sayılarla Çok Adımlı İşlemler
Rasyonel sayılarla iki veya daha fazla işlem içeren ifadelere çok adımlı işlemler denir. Bu işlemlerde hangi adımın daha önce yapılacağını belirlemek için ”( )” yada ”[ ]” gibi ayıraçlar kullanılır.
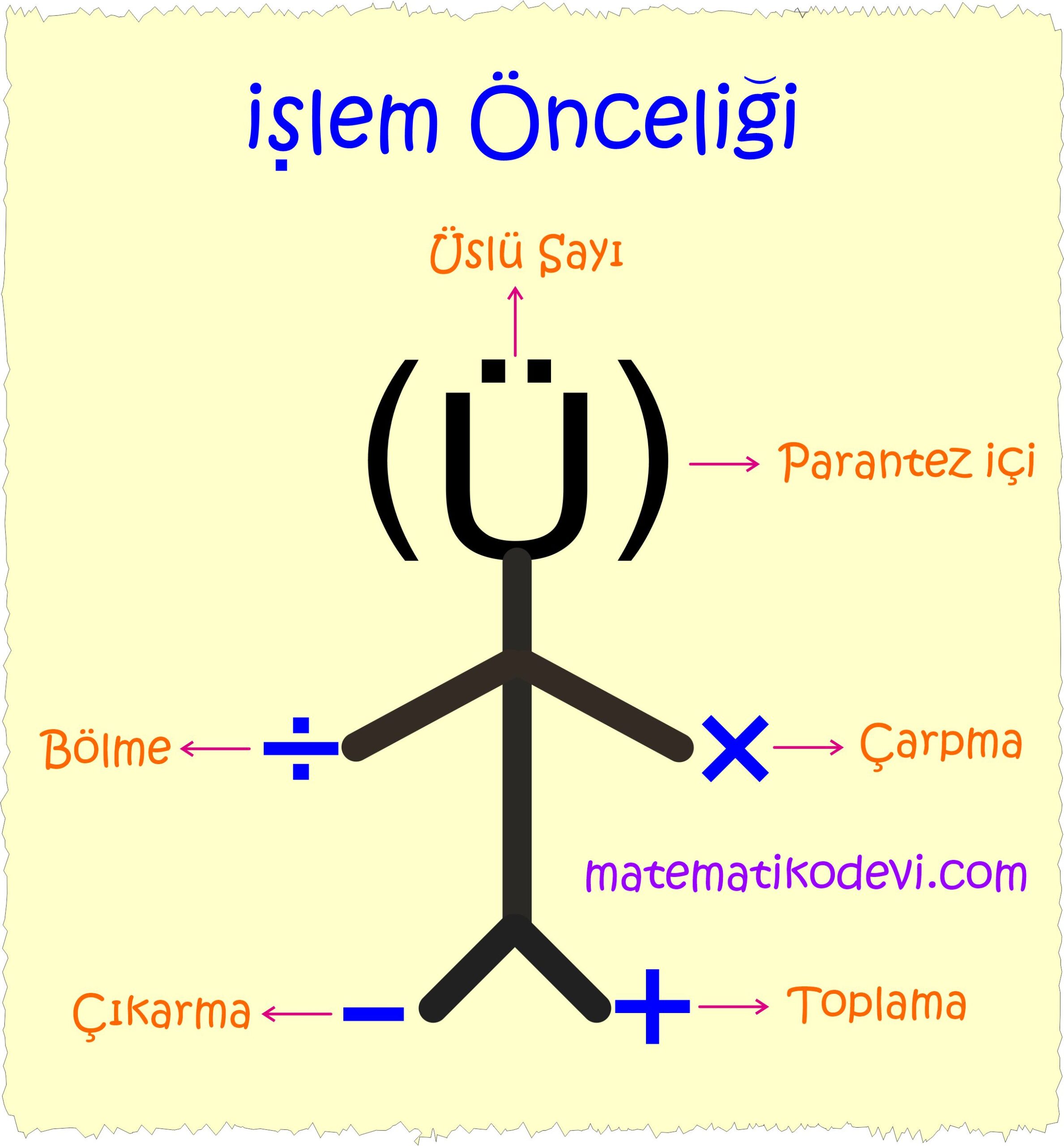
Çok adımlı işlemler birden fazla işlem içerdiği için işlem önceliği basamaklarına dikkat etmeliyiz.
Birden fazla işlemin olduğu durumlarda aşağıda sıraya göre işlem basamakları yapılır.
- Üslü Sayı
- Parantez içi
- Çarpma ve Bölme
- Toplama ve Çıkarma
Rasyonel sayılarla çok adımlı işlemler nasıl çözülür?
✅ Birden çok işlem varsa işlem önceliğine dikkat ederiz.
Örneğin;
\dfrac{7}{3} + [\dfrac{3}{2} – \dfrac{5}{21} × \dfrac{7}{5}]
- Yukarıdaki örnek birden çok işlem içermektedir. İşlem önceliğine göre parantez içinden işleme başlanır. Parantez içinde çıkarma ve çarpma işlemleri var. Parantez içinde de işlem önceliğine dikkat ederiz. O zaman parantez içinde çarpma işlemini önce yaparız.
\dfrac{5}{21} × \dfrac{7}{5} = \dfrac{1}{3}
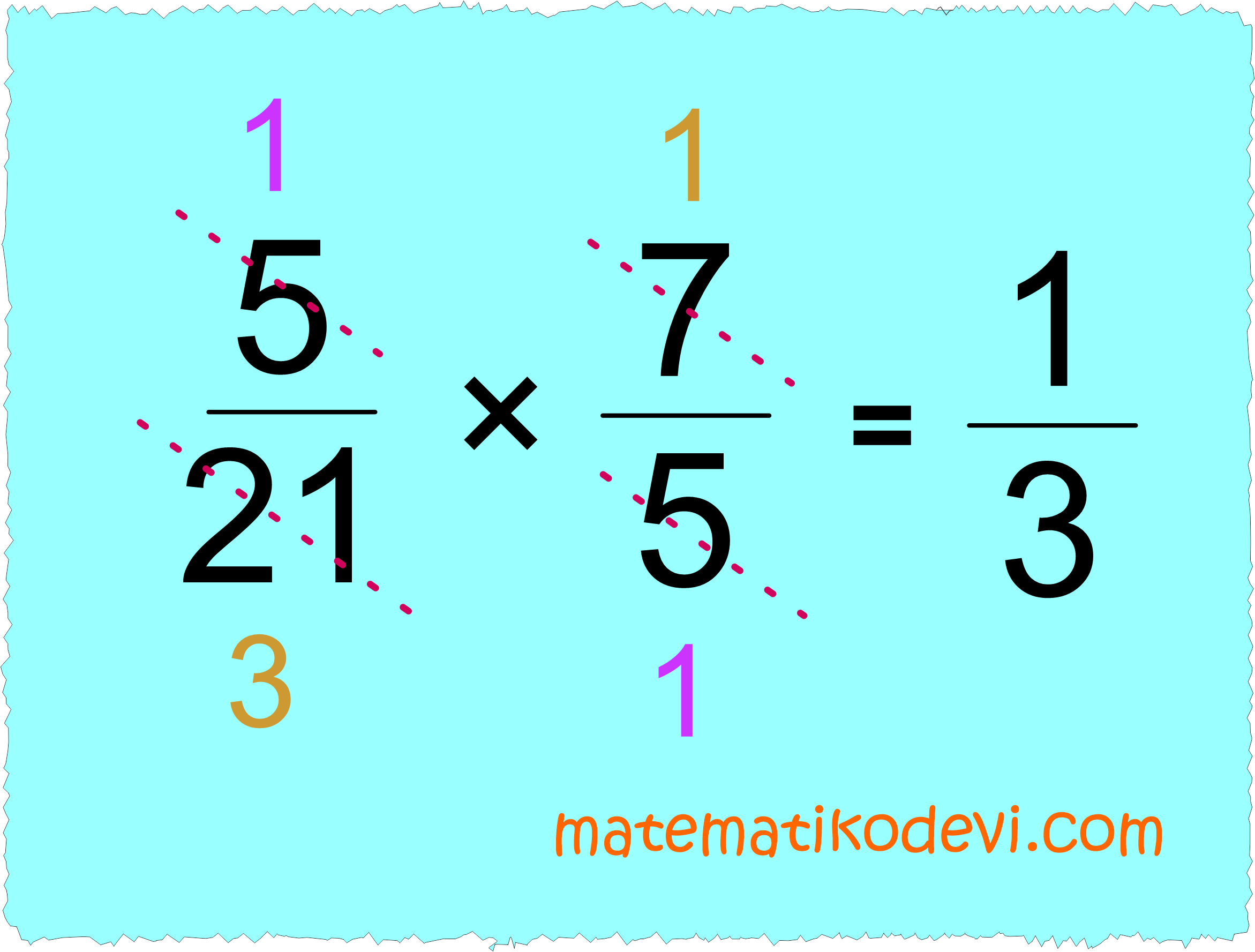
- Daha sonra parantez içindeki çıkarma işlemini yaparız.
\dfrac{3}{2} – \dfrac{1}{3}
\dfrac{3×3}{2×3} – \dfrac{1×2}{3×2}
\dfrac{9}{6} – \dfrac{2}{6}
\dfrac{7}{6}
- En son bulduğumuz rasyonel sayı ile parantez dışındaki rasyonel sayıyı toplarız.
\dfrac{7}{3} + \dfrac{7}{6}
\dfrac{7×2}{3×2} + \dfrac{7}{6}
\dfrac{14}{6} + \dfrac{7}{6}
\dfrac{21}{6}
Rasyonel Sayılarda Merdivenli İşlemler Nasıl Çözülür?
✅ Sadece kesir çizgisinin bulunduğu işlemlerde ” = ” sembolünün hizasında bulunan işlemlerde ;
- Önce büyük kesir çizgisinin payında ve paydasında bulunan işlemleri yaparız.
- Sonra pay kısmında bulunan sonucu, payda kısmında bulunan sonuca böleriz.
Örneğin;
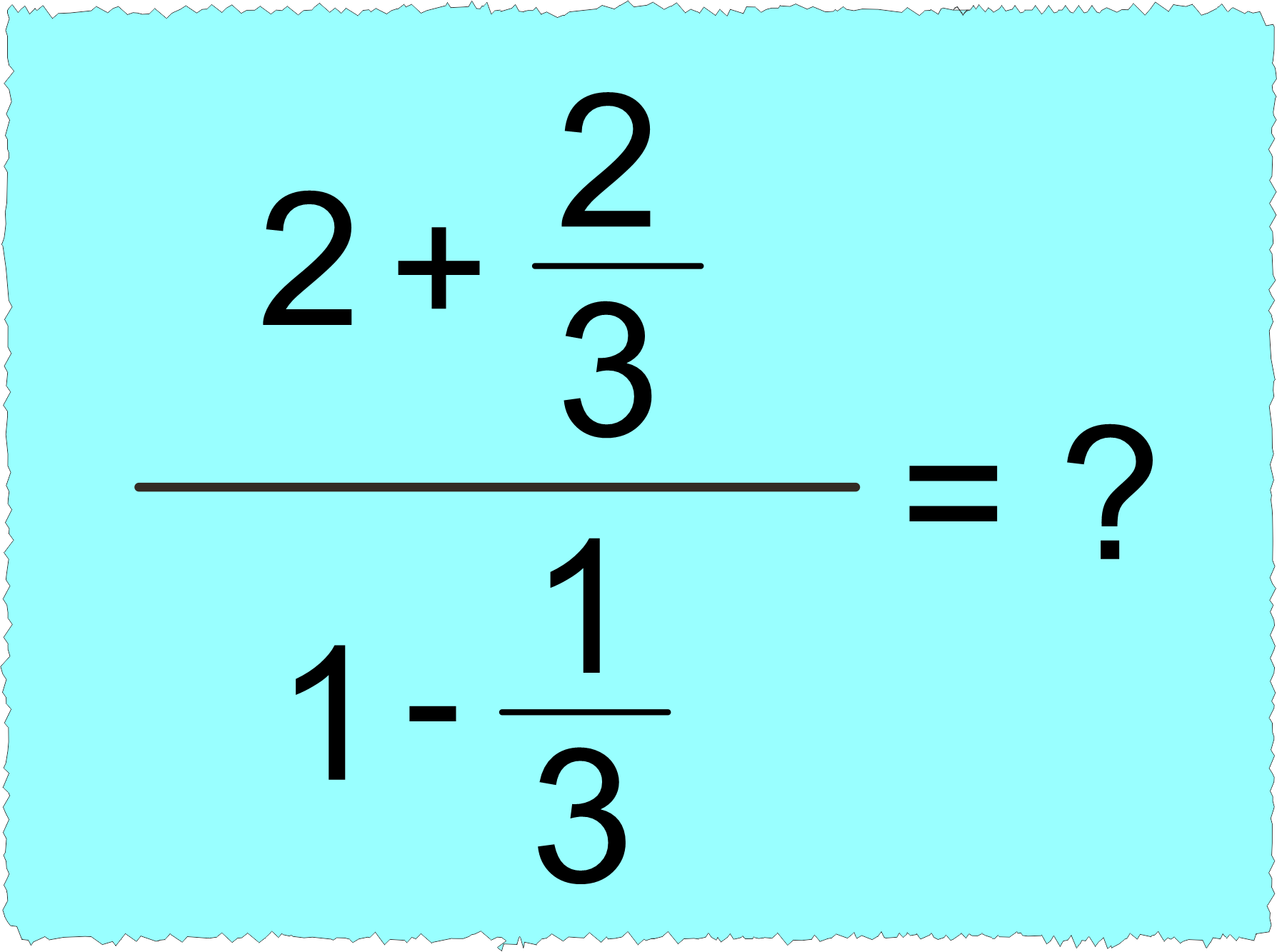
Yukarıdaki işlemin sonucunu bulalım.
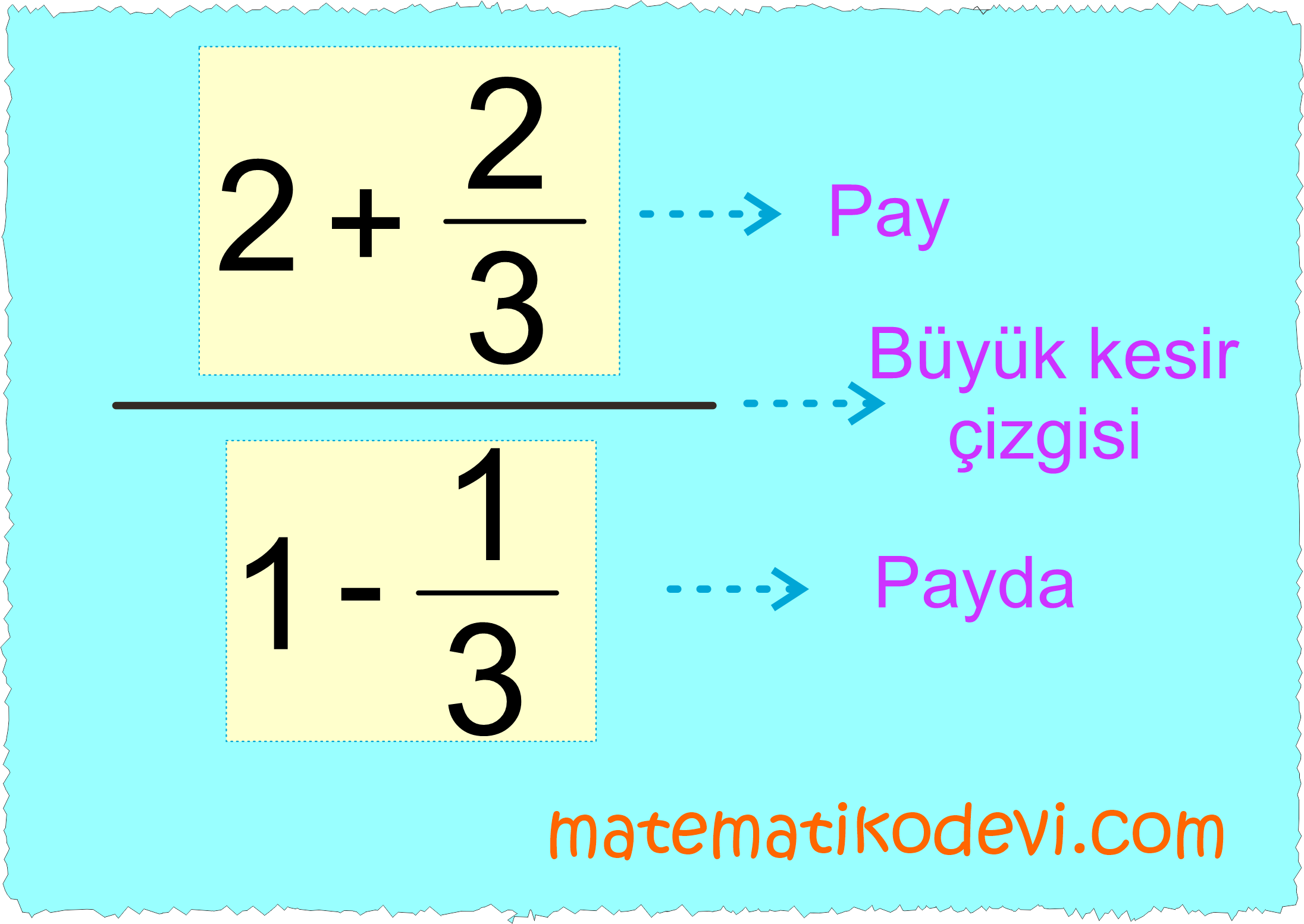
➡️ Pay kısmında bulunan işlemi yapalım.
2+ \dfrac{2}{3} = \dfrac{8}{3}
➡️ Payda kısmında bulunan işlemi yapalım.
1- \dfrac{1}{3} = \dfrac{2}{3}
➡️Pay kısmında bulunan sonucu, payda kısmında bulunan sonuca böleriz.
\dfrac{8}{3} ÷ \dfrac{2}{3}
\dfrac{8}{3} × \dfrac{3}{2}
\dfrac{24}{6}
4
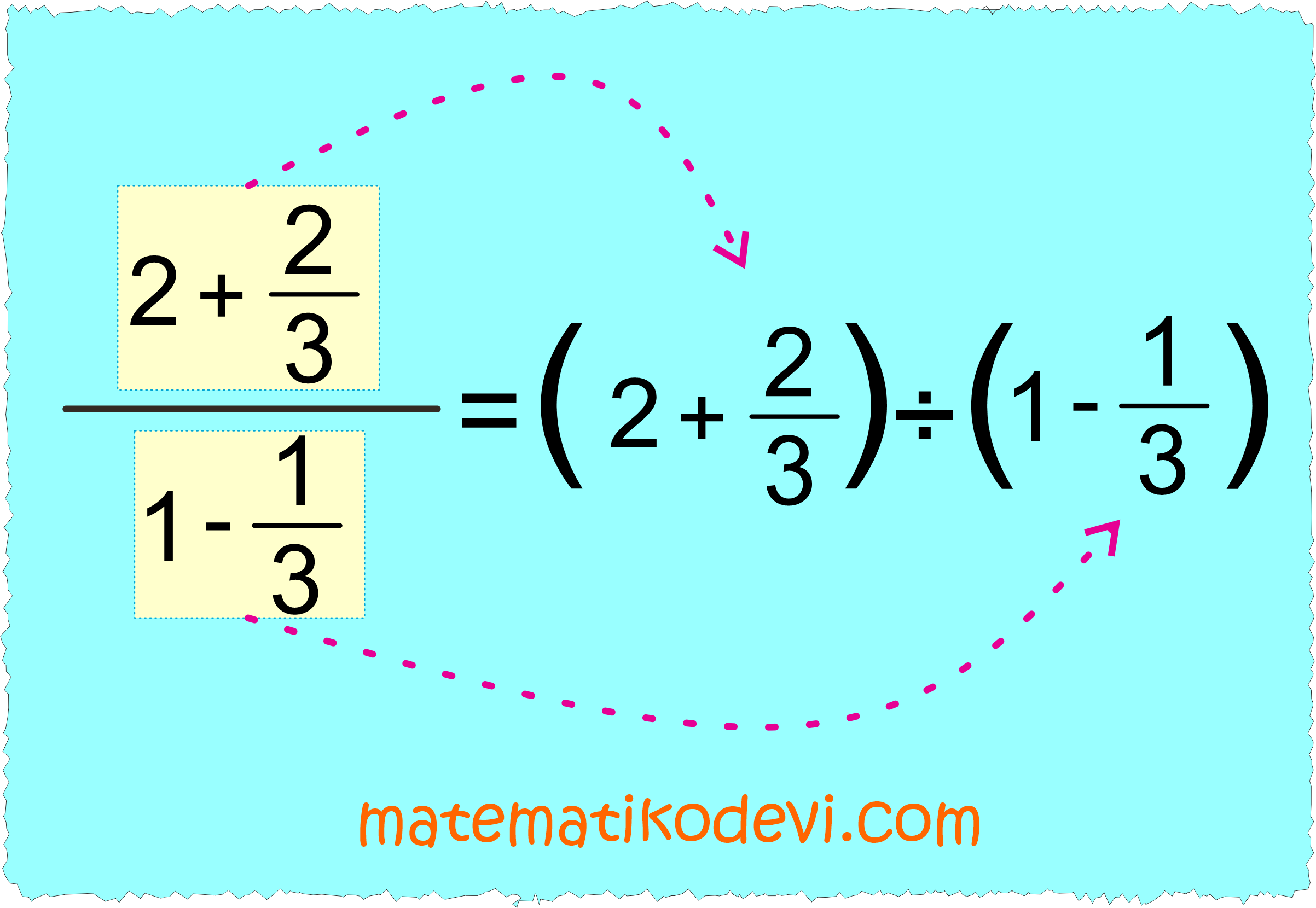
✅ Toplama veya çıkarma işleminin hizasında bulunan kesir çizgisi hangi iki rasyonel sayının birbirine bölüneceğini gösterir.
Örneğin;
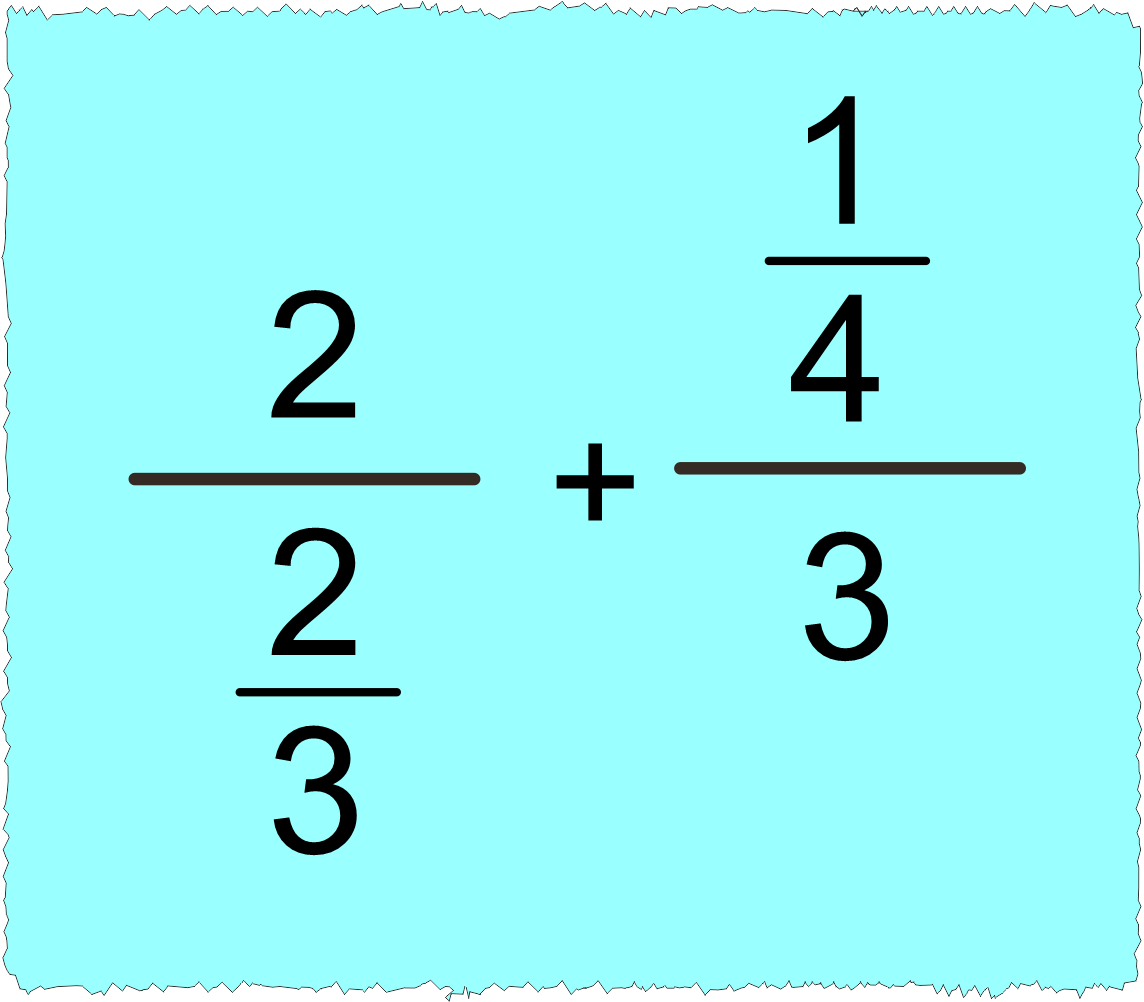
Yukarıdaki işlemin sonucunu bulalım.
➡️ Toplama işleminin hizasına bakalım.
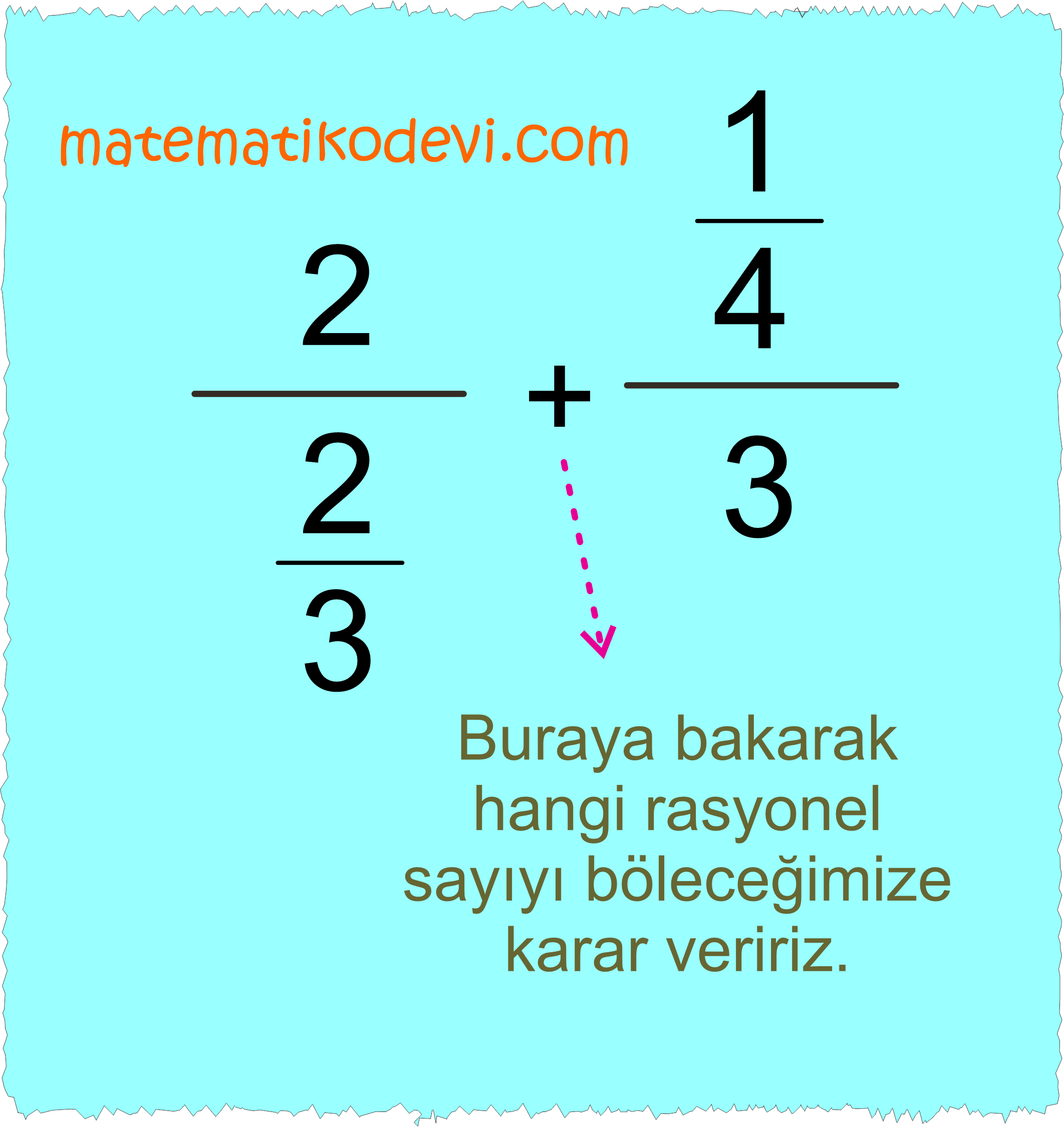
➡️ Toplama işleminin hizasına bakarak rasyonel sayılarını bölme işlemi olarak yazalım.
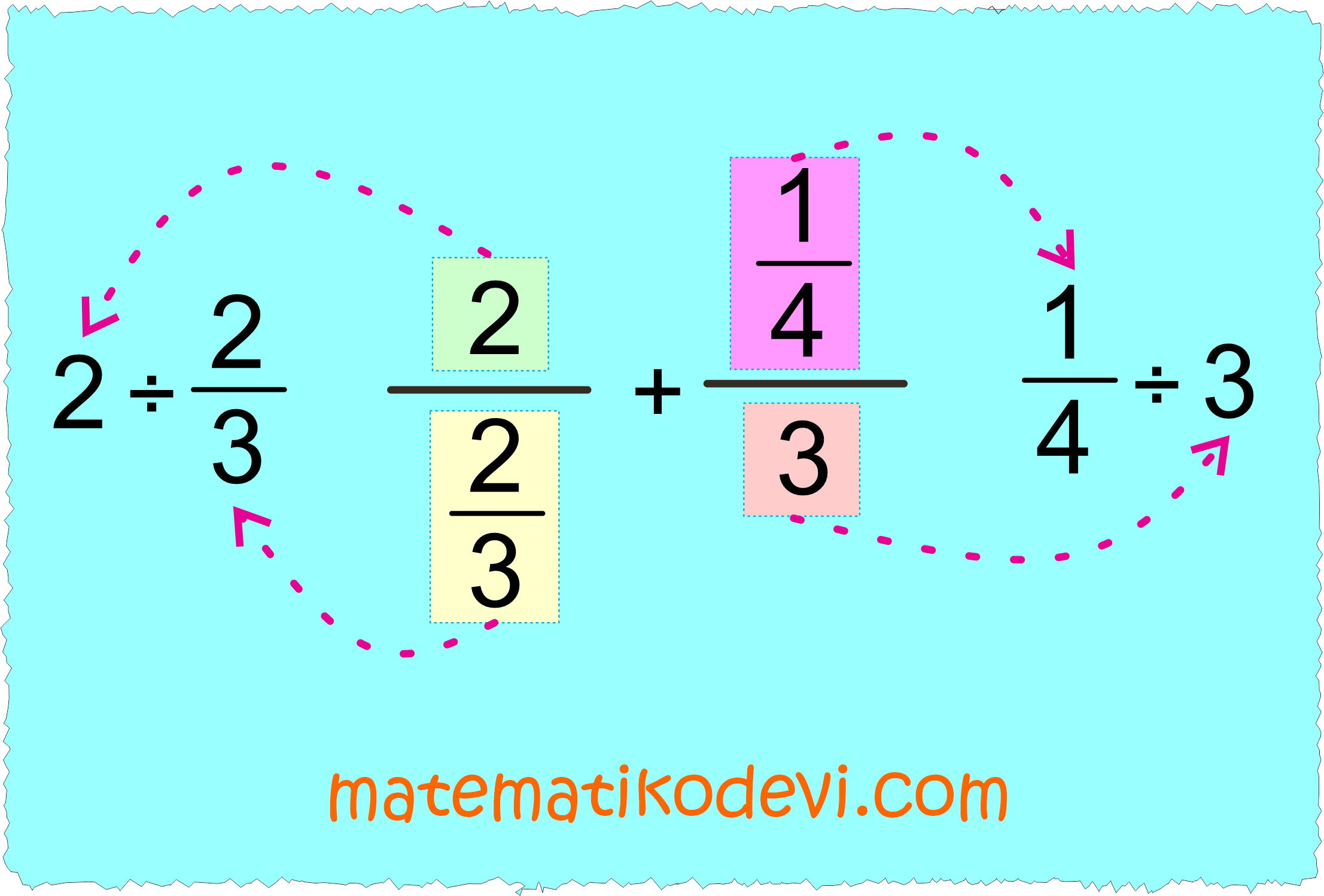
( 2 ÷ \dfrac{2}{3} ) + ( \dfrac{1}{4} ÷ 3 )
➡️ Şimdi parantez içindeki işlemleri yapalım.
2 ÷ \dfrac{2}{3}
\dfrac{2}{1} × \dfrac{3}{2}
\dfrac{6}{2}
3
\dfrac{1}{4} ÷ 3
\dfrac{1}{4} × \dfrac{1}{3}
\dfrac{1}{12}
➡️ Şimdi bulduğumuz sonuçları toplayalım.
3 + \dfrac{1}{12}
3 \dfrac{1}{12} = \dfrac{37}{12}
✅ Birden fazla kesir çizgisi içeren merdivenli işlemlerde merdivenin en küçük basamağından, en büyük basamağına doğru adım adım işlemler yapılır. Yani en alt basamaktan işleme başlayarak adım adım ilerleriz.
Örneğin;
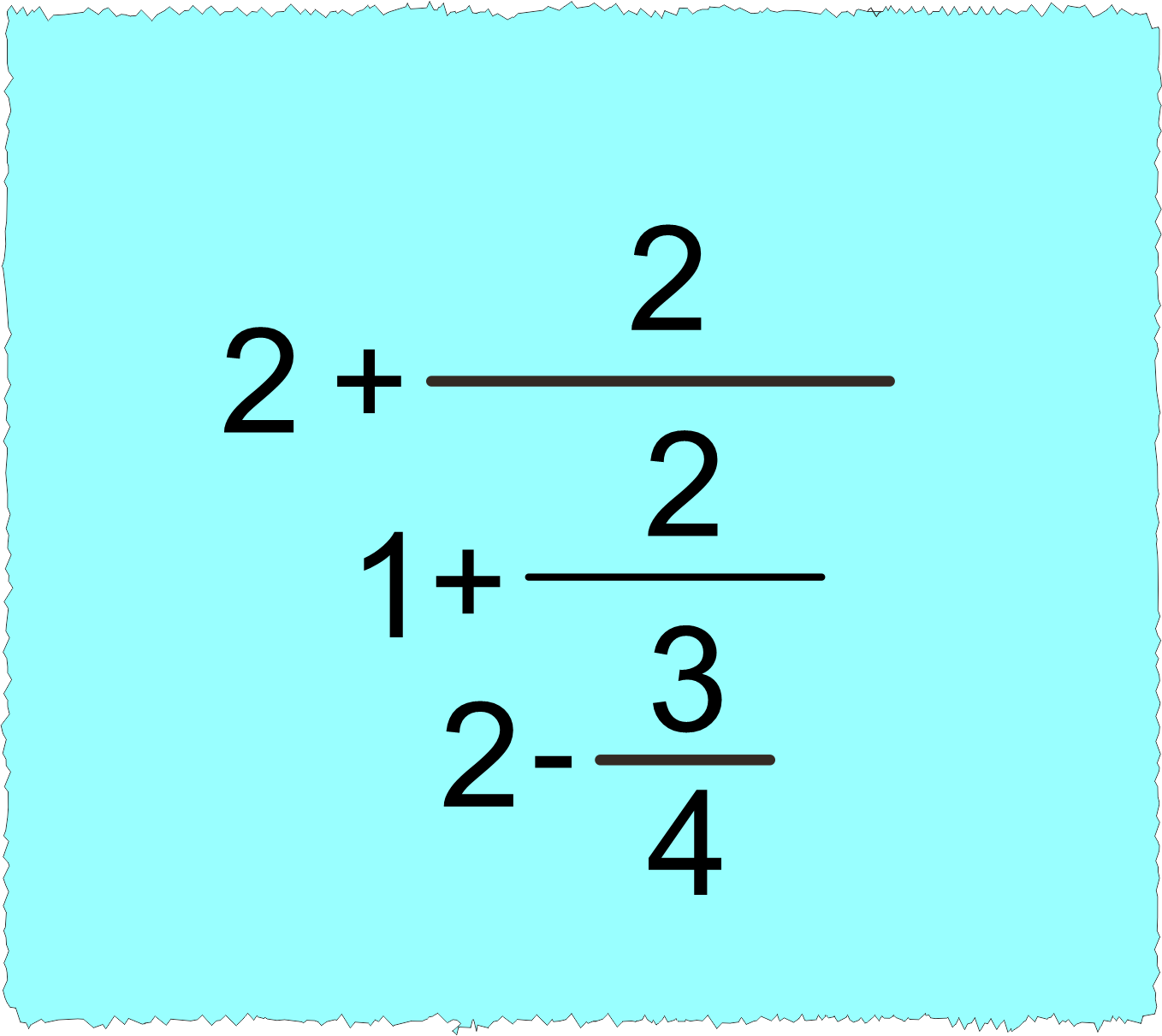
Yukarıdaki işlemin sonucunu bulalım.
➡️ İşleme en alt basamaktan başlayalım.
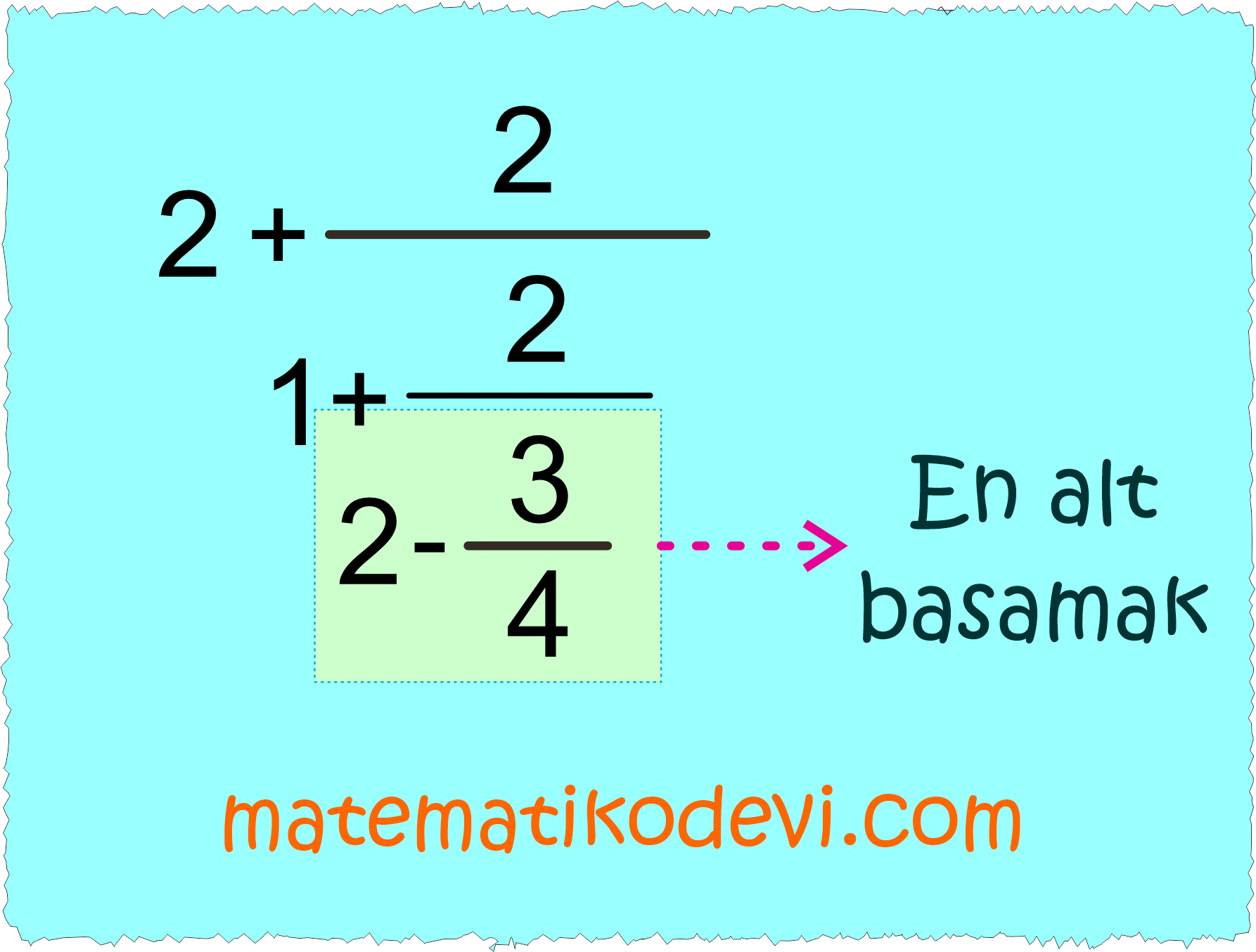
2 – \dfrac{3}{4}
\dfrac{2}{1} – \dfrac{3}{4}
\dfrac{8}{4} – \dfrac{3}{4}
\dfrac{5}{4}
➡️ Şimdi bulduğumuz sonucu yazıp bir basamağın işlemini yapalım.
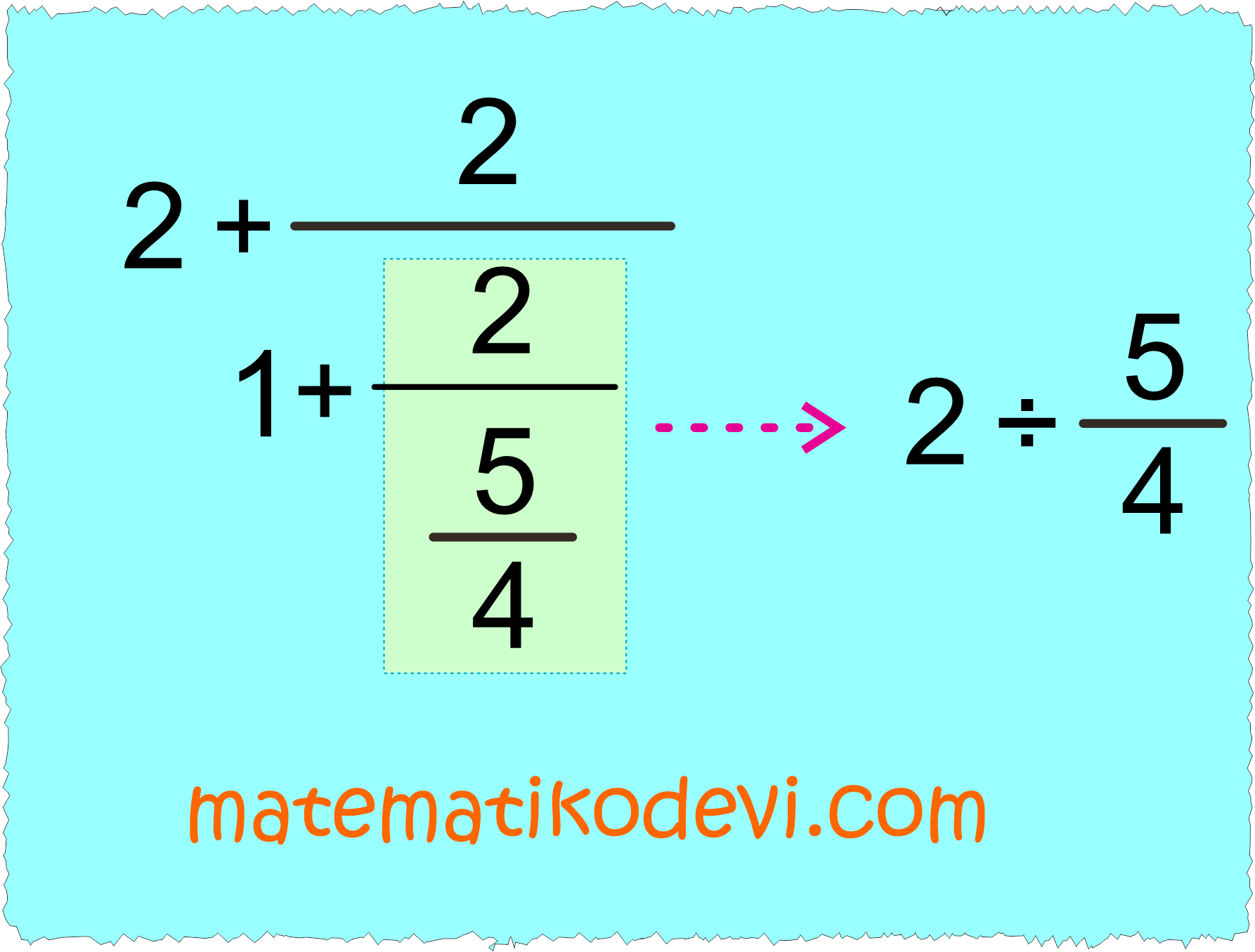
2÷ \dfrac{5}{4}
\dfrac{2}{1} ÷ \dfrac{5}{4}
\dfrac{2}{1} × \dfrac{4}{5}
\dfrac{8}{5}
➡️ Bulduğumuz sonucu 1 ile toplayalım.
1+ \dfrac{8}{5}
1 \dfrac{8}{5} = \dfrac{13}{5}
➡️ Bulduğumuz sonucu bir üst basamağa yazıp sonucu bulalım.
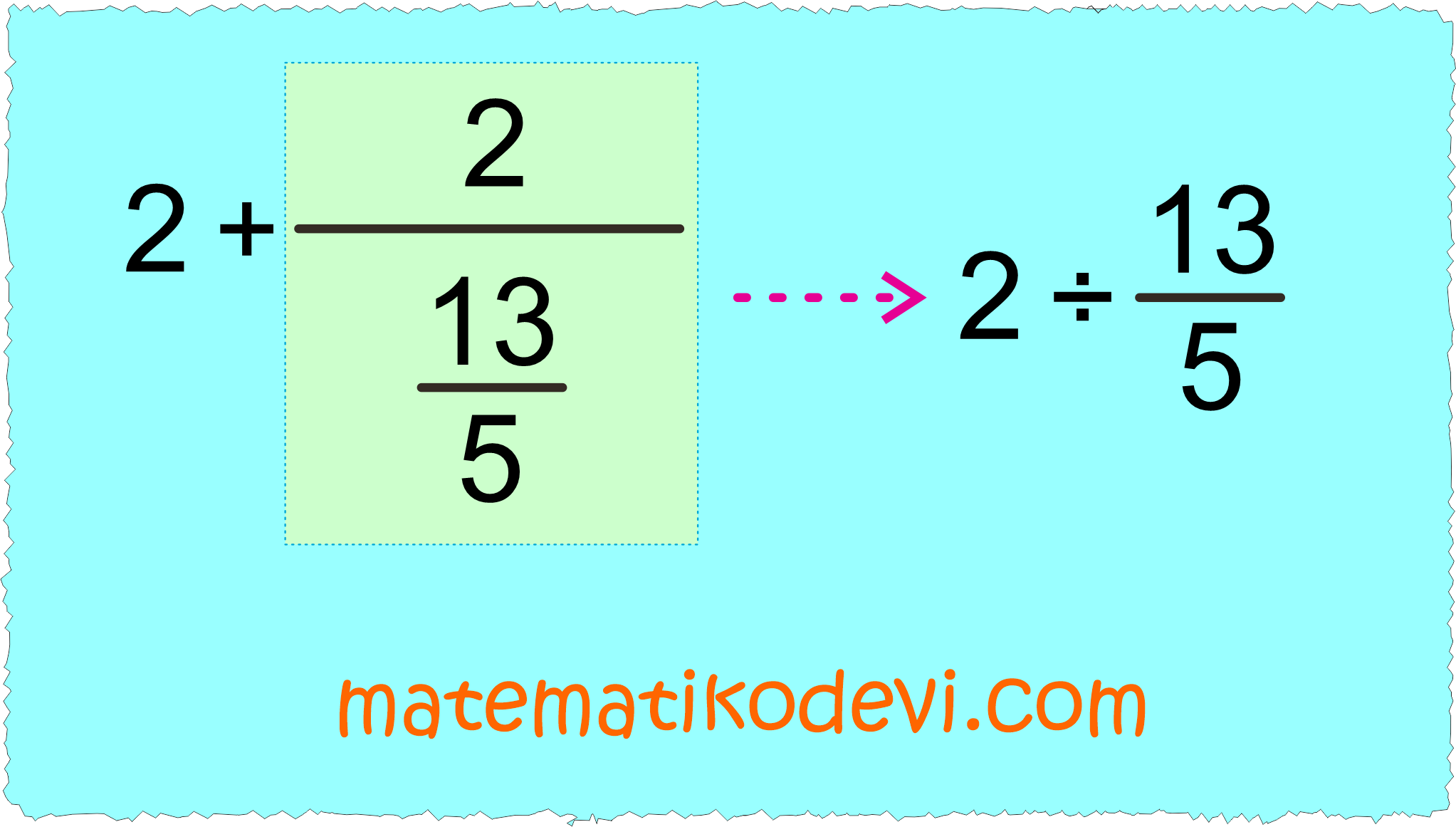
2÷ \dfrac{13}{5}
\dfrac{2}{1} ÷ \dfrac{13}{5}
\dfrac{2}{1} × \dfrac{5}{13}
\dfrac{10}{13}
➡️ Bulduğumuz sonucu 2 ile toplayalım.
2 + \dfrac{10}{13}
2 \dfrac{10}{13} = \dfrac{36}{13}
Rasyonel Sayılarda Bilinmeyen Nasıl Bulunur?
✅ Rasyonel bilinmeyeni bulmayı bir örnek ile açıklayalım.
Örneğin;
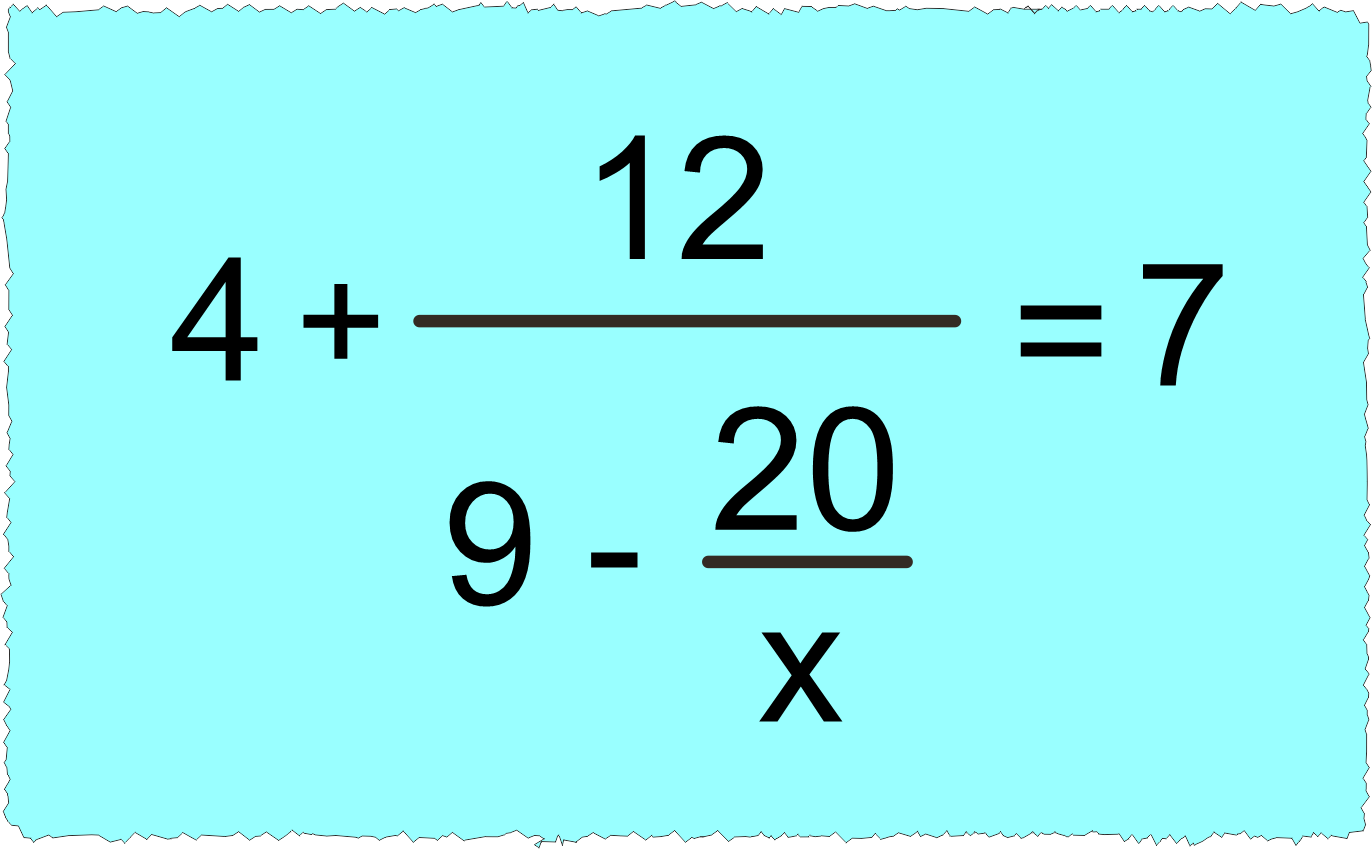
Yukarıda verilen işlemde bilinmeyeni (x) bulalım.
➡️ 4 ile bir sayıyı topladığımızda 7 olmuş. ” 4 ile hangi sayıyı toplarsak 7 olur? ” sorusunun cevabını bulmamız gerekir.
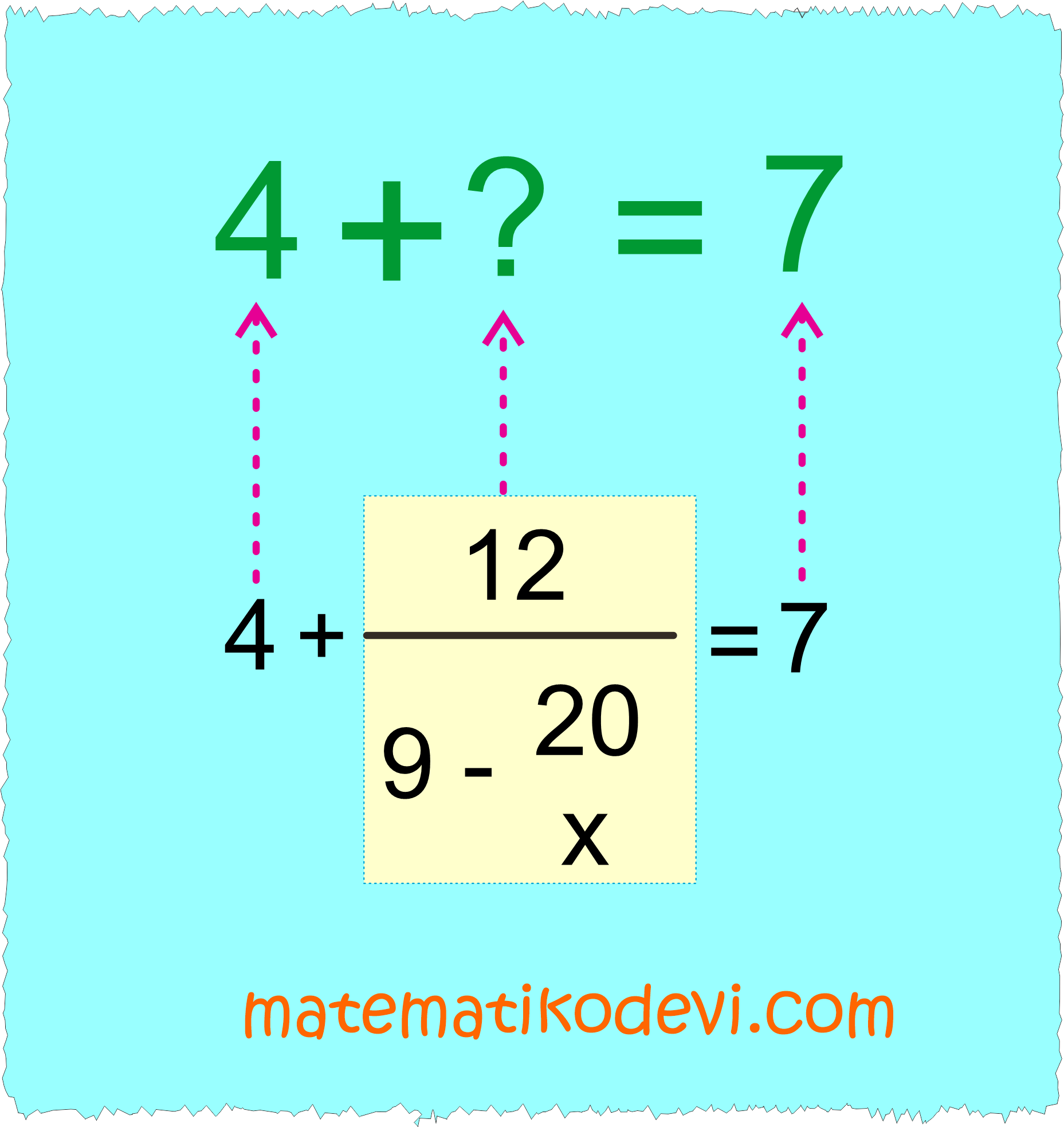
🤓 Yukarıdaki görseli incelediğimizde sarı renk ile gösterilen ifade 3 olur.
➡️ İşlem aşağıdaki gibi olur.
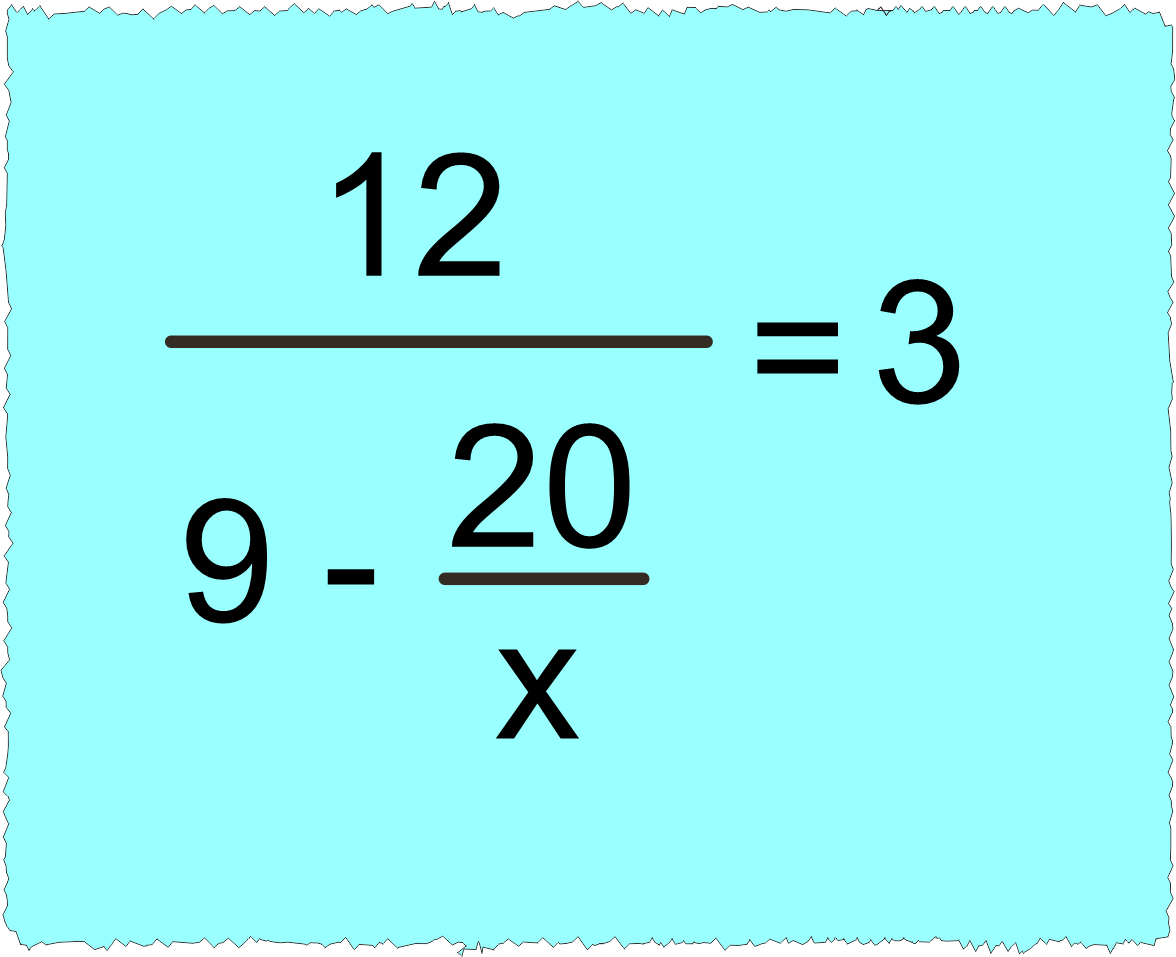
➡️ Bu işlemi çözmek için ”12’yi kaça bölersek sonuç 3 olur?” sorusunu sormalıyız.
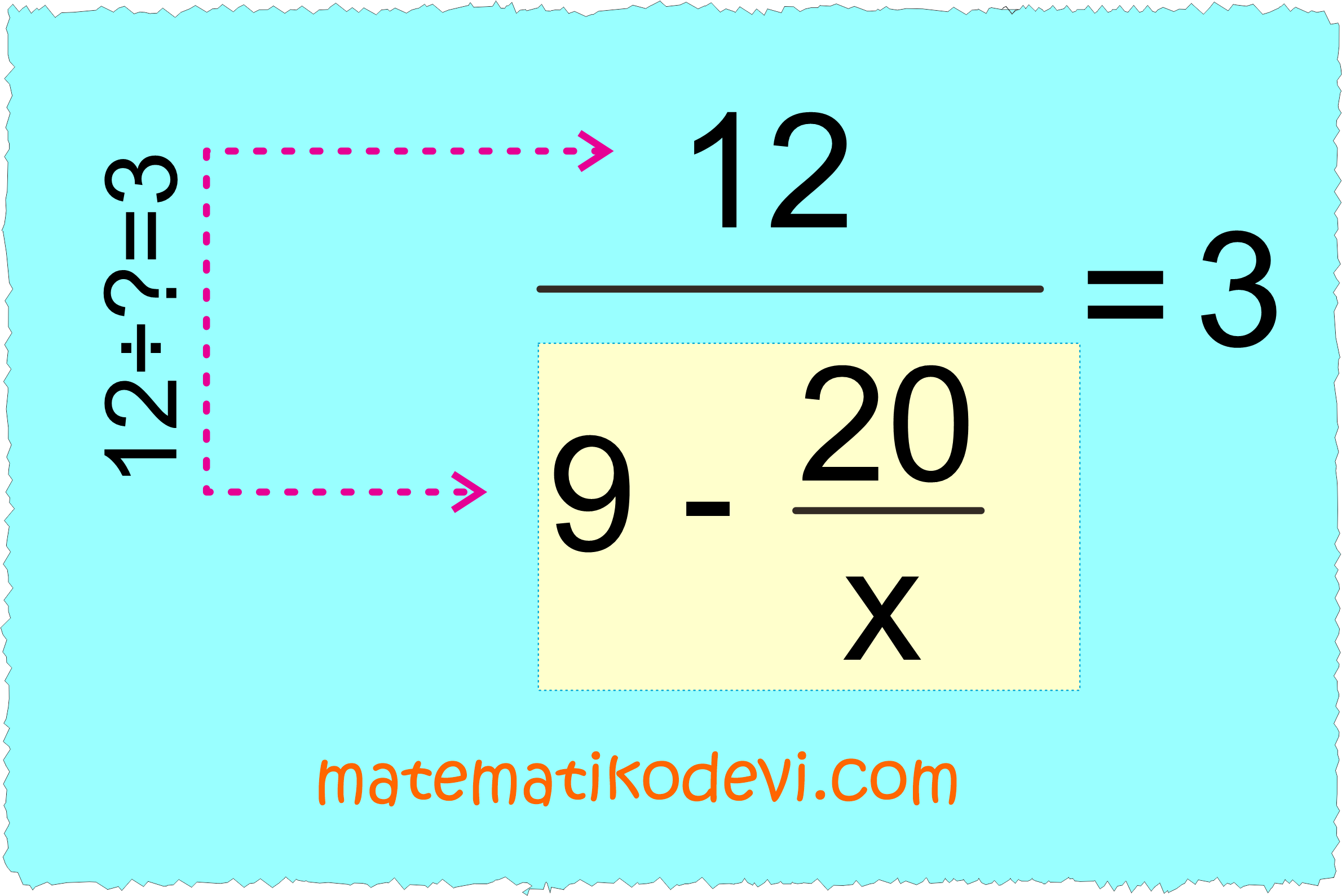
🤓 Yukarıdaki görseli incelediğimizde sarı renk ile gösterilen ifade 4 olur.
➡️ İşlem aşağıdaki gibi olur.
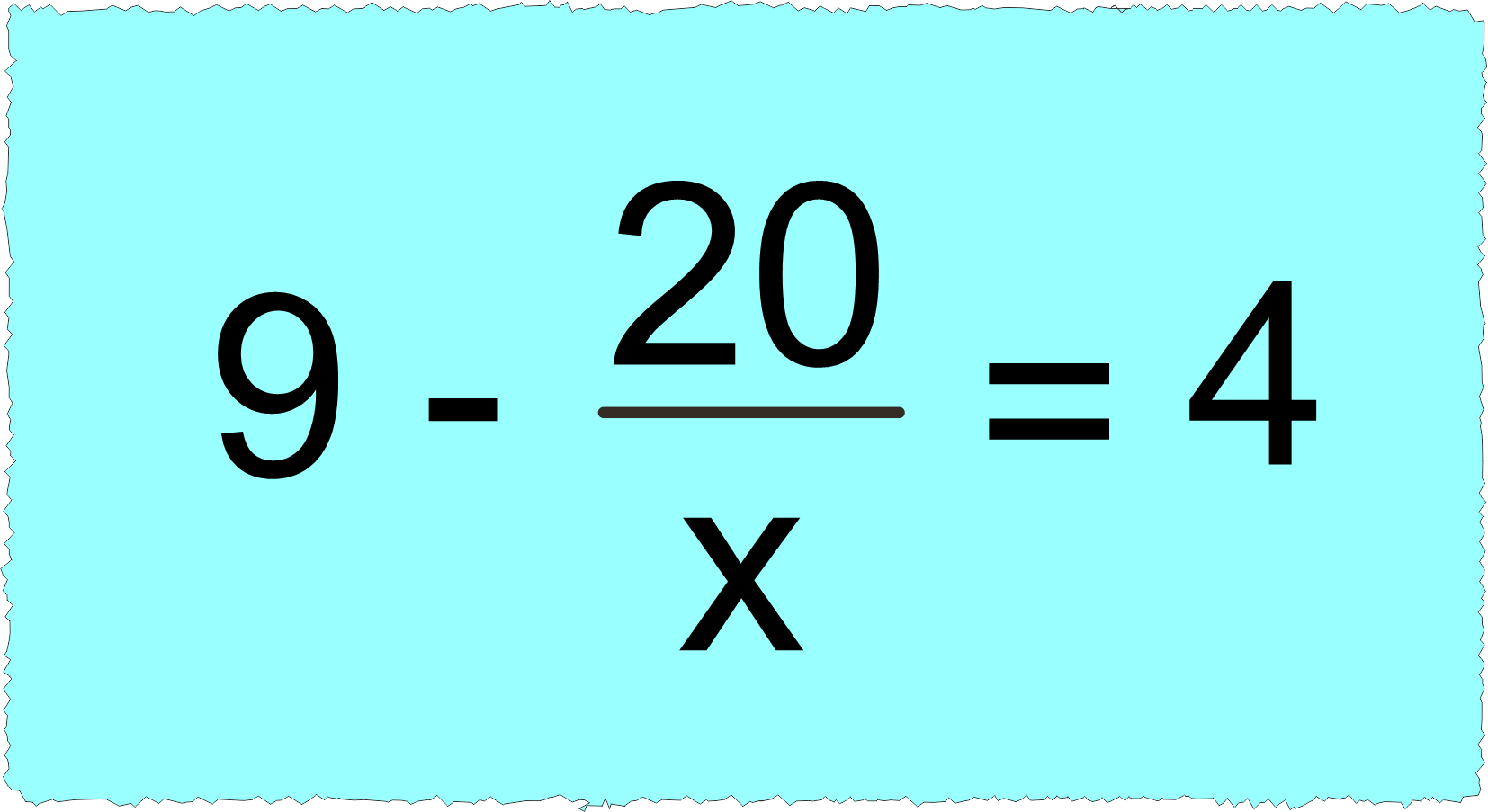
➡️ Bu işlemi çözmek için ”9’dan kaç çıkarırsak sonuç 4 olur?” sorusunu sormalıyız.
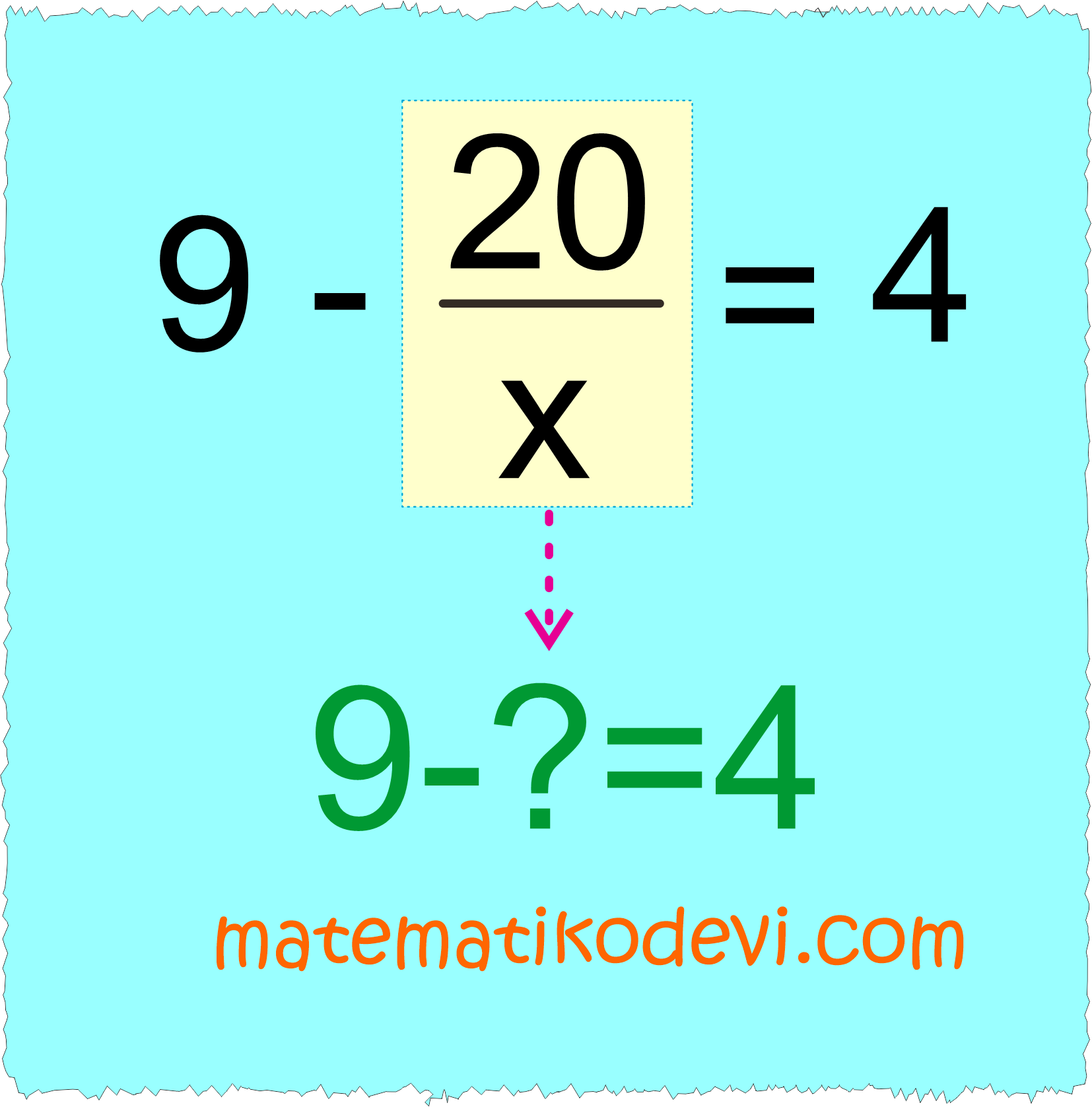
🤓 Yukarıdaki görseli incelediğimizde sarı renk ile gösterilen ifade 5 olur.
➡️ İşlem aşağıdaki gibi olur.
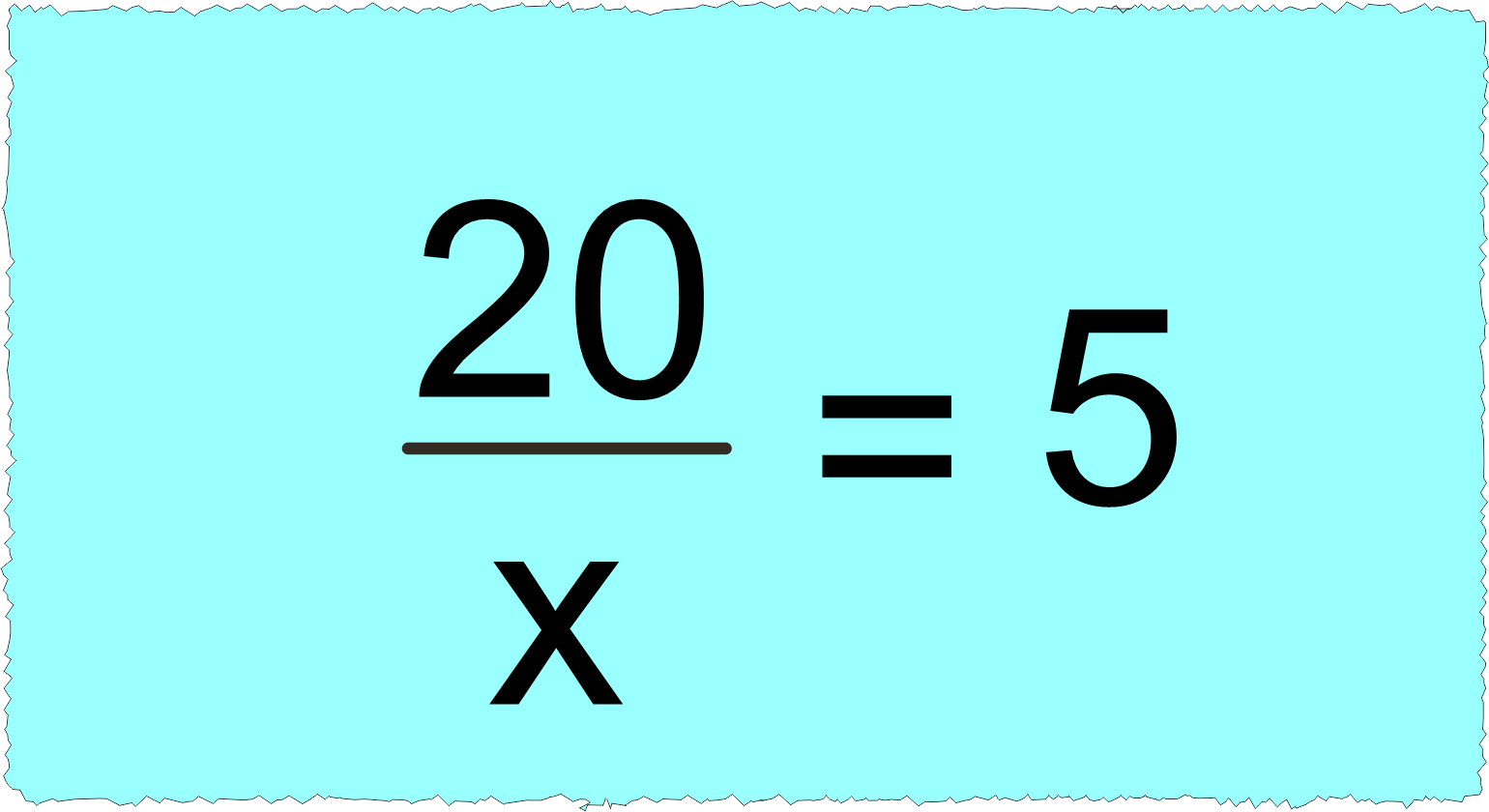
➡️ Bu işlemi çözmek için ”20’yi kaça bölersek 5 olur?’ sorusunu sormalıyız.
Bu sorunun cevabı olan 4 bilinmeyenin cevabıdır.
Yani x=4 olur.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Rasyonel Sayılarla Çarpma ve Bölme İşlemi | Bir Rasyonel Sayının Karesi ve Küpü Konu Anlatımı |

