Rasyonel Sayılarla Çarpma ve Bölme İşlemi
Kazanım: Rasyonel sayılarla çarpma ve bölme işlemlerini yapar.
Bu konuda neler öğreneceğiz :
Rasyonel Sayılarla Çarpma ve Bölme İşlemi
Rasyonel sayılarla çarpma ve bölme işlemleri konu anlatımı aşağıda yapılmıştır.
Rasyonel Sayılarla Çarpma İşlemi
Rasyonel sayılarla çarpma işlemi yaparken;
- Payların çarpımı paya, paydaların çarpımı ise paydaya yazılır.
Örneğin;
\dfrac{3}{4} ×(- \dfrac{2}{5} )
– \dfrac{3×2}{4×5}
– \dfrac{6}{20}
Çarpılan sayılarda tam sayılı kesir varsa bileşik kesre çevrilir, sonra çarpma yapılır.,
Örneğin;
1 \dfrac{2}{3} × \dfrac{1}{2}
➡️ Tam sayılı kesri bileşik kesre çeviririz.
1 \dfrac{2}{3} = \dfrac{5}{3}
➡️ Sonra çarpma yaparız.
\dfrac{5}{3} × \dfrac{1}{2}
\dfrac{5×1}{3×2}
\dfrac{5}{6}
Çarpılan sayılardan birinde tam sayı varsa tam sayının paydasına 1 yazılıp çarpma işlemi yapılır.
Örneğin;
4× \dfrac{3}{7}
➡️ çarpanlardan biri tam sayı olduğu için tam sayının paydasına 1 yazarız.
Örneğin;
\dfrac{4}{1} × \dfrac{3}{7}
\dfrac{4×3}{1×7}
\dfrac{12}{7}
Not: Çarpma işlemini yaptıktan sonra varsa sadeleştirme yaparız. Sadeleştirmeyi çarpmayı yapmadan öncede yapabiliriz.
Rasyonel Sayılarla Bölme İşlemi
Rasyonel sayılarda bölme işlemini birinci kesri aynen yazıp ikinci kesri ters çevirip çarpabiliriz veya paydaları eşitleyip payları oranlayabiliriz. Bu yöntemler aşağıda detaylı anlatılmıştır.
Birinci Kesri Aynen Yazıp İkinci Kesri Ters Çevirip Çarpma Yöntemi:
Rasyonel sayılarda bölme işlemini yaparken;
- Birinci kesir aynen yazılır.
- İkinci kesir ters çevrilip çarpılır.
Örneğin;
(- \dfrac{3}{5} )÷ \dfrac{1}{4}
➡️ Birinci kesri aynen yaz, ikinci kesri ters çevirip çarp.
(- \dfrac{3}{5} )× \dfrac{4}{1}
– \dfrac{3×4}{5×1}
– \dfrac{12}{5}
Bölünen sayılarda tam sayılı kesir varsa tam sayılı kesir bileşik kesre çevrilir sonra çarpma yapılır.
Örneğin;
2 \dfrac{1}{3} ÷ \dfrac{1}{2}
➡️ Tam sayılı kesri bileşik kesre çeviririz.
2 \dfrac{1}{3} = \dfrac{7}{3}
\dfrac{7}{3} ÷ \dfrac{1}{2}
➡️ Birinci kesri aynen yaz, ikinci kesri ters çevirip çarp.
\dfrac{7}{3} × \dfrac{2}{1}
\dfrac{14}{3}
Bölünen sayılardan biri tam sayı ise tam sayının paydasına 1 yazıp çarpmayı yaparız.
Örneğin;
\dfrac{3}{8} ÷3
➡️ Tam sayının paydasına 1 yazarız.
\dfrac{3}{8} ÷ \dfrac{3}{1}
➡️ Birinci kesri aynen yaz, ikinci kesri ters çevirip çarp.
\dfrac{3}{8} × \dfrac{1}{3}
\dfrac{3}{24} = \dfrac{1}{8}
Not: Bölme işlemini yaparken çarpmaya dönüştürdükten sonra sadeleştirme yapabiliriz veya çarpmayı yaptıktan sonra sadeleştirme yapabiliriz.
Paydaları Eşitleme Yöntemi:
Rasyonel sayılarda bölme işlemini yaparken;
- Rasyonel sayıların paydalarını eşitleriz.
- Birinci kesrin payını, paya yazarız.
- İkinci kesrin payını, paydaya yazarız.
Örneğin;
\dfrac{3}{4} ÷ \dfrac{2}{3}
➡️ Paydalarını eşitleyelim.
\dfrac{3×3}{4×3} ÷ \dfrac{2×4}{3×4}
\dfrac{9}{12} ÷ \dfrac{8}{12}
➡️ Birinci kesrin payını paya, ikinci kesrin payını paydaya yazarız.
\dfrac{9}{8}
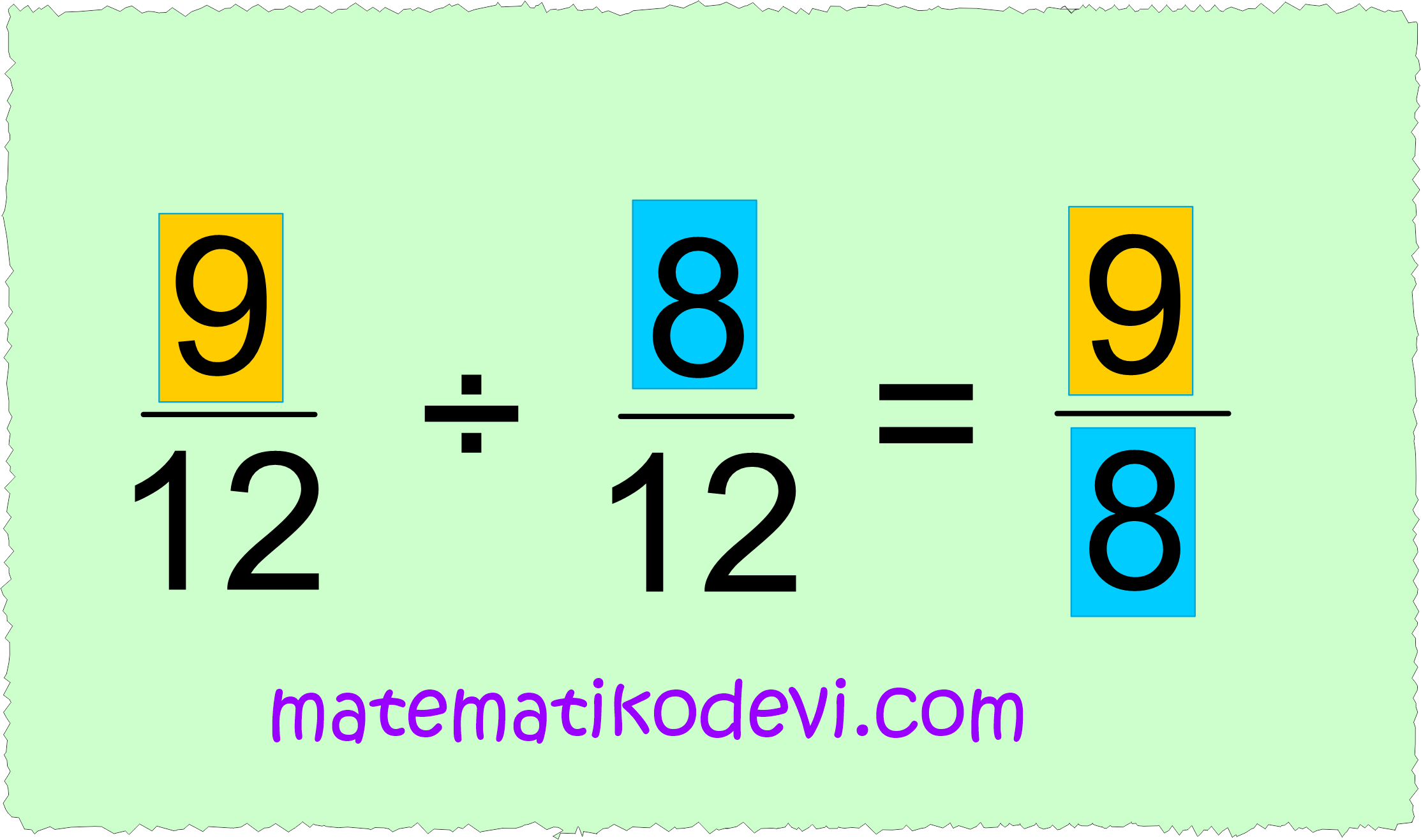
Sıfır sayısını bir sayıya (sıfır hariç) böldüğümüzde sonuç sıfır olur.
Örneğin;
0÷ \dfrac{6}{7} = 0
0÷3 \dfrac{4}{9} = 0
Bir sayıyı sıfıra böldüğümüzde sonuç tanımsız olur.
Örneğin;
\dfrac{4}{11} ÷0 = Tanımsız
6 \dfrac{2}{5} ÷0 = Tanımsız
1 sayısını kesirli bir sayıya böldüğümüzde sonuç kesirli sayının tersi olur.
Örneğin;
1÷ \dfrac{5}{8} = \dfrac{8}{5}
1÷(- \dfrac{3}{4} ) = (- \dfrac{4}{3} )
Bir sayıyı 1’e böldüğümüzde sonuç sayının kendisi olur.
Örneğin;
\dfrac{4}{7} ÷1 = \dfrac{4}{7}
4 \dfrac{2}{3} ÷1 = 4 \dfrac{2}{3}
Rasyonel Sayılarla Çarpma İşleminin Özellikleri
Rasyonel sayılarda çarpılan sayıların yeri değiştiğinde sonuç değişmez. Yani rasyonel sayılarda çarpma işleminin değişme özelliği vardır.
- \dfrac{a}{b} × \dfrac{c}{d} = \dfrac{c}{d} × \dfrac{a}{b}
Örneğin;
\dfrac{5}{4} × \dfrac{2}{3} = \dfrac{2}{3} × \dfrac{5}{4}
Not: Rasyonel sayılarda bölme işleminde değişme özelliği yoktur.
Herhangi bir rasyonel sayıyı 1 ile çarptığımızda sonuç değişmez. Yani rasyonel sayılarda çarpma işleminin etkisiz elemanı 1’dir.
- \dfrac{a}{b} ×1 = \dfrac{a}{b}
Örneğin;
(- \dfrac{8}{11} )×1 = – \dfrac{8}{11}
Herhangi bir rasyonel sayıyı 0 ile çarptığımızda sonuç 0 olur. Yani rasyonel sayılarda çarpma işleminin yutan elemanı 0’dır.
- \dfrac{a}{b} ×0 = 0
Örneğin;
3 \dfrac{2}{9} ×0 =0
Çarptığımızda sonucu 1 olan iki rasyonel sayı çarpma işlemine göre birbirinin tersidir. Bu duruma ters eleman özelliği denir.
- \dfrac{a}{b} × \dfrac{b}{a} = 1 olduğu için
- \dfrac{a}{b} rasyonel sayısının çarpma işlemine göre tersi \dfrac{b}{a} olur.
Örneğin;
\dfrac{2}{5} × \dfrac{5}{2} = 1 olduğu için
\dfrac{2}{5} rasyonel sayısının çarpma işlemine göre tersi \dfrac{5}{2} olur.
Üç ya da daha fazla rasyonel sayıyı ile çarpma işlemi yapılırken, öncelikle hangi iki rasyonel sayının çarpılacağının sonuca bir etkisi yoktur. Yani rasyonel sayılarda çarpma işleminin birleşme özelliği vardır.
- ( \dfrac{a}{b} × \dfrac{c}{d} ) × \dfrac{e}{f} = \dfrac{a}{b} × ( \dfrac{c}{d} × \dfrac{e}{f} )
Örneğin;
(\dfrac{1}{2} × \dfrac{2}{3} ) × \dfrac{5}{6} = \dfrac{1}{2} × (\dfrac{2}{3} × \dfrac{5}{6} )
\dfrac{2}{6} × \dfrac{5}{6} = \dfrac{1}{2} × \dfrac{10}{18}
\dfrac{10}{36} = \dfrac{10}{36}
Bir rasyonel sayıyı parantez içinde toplanan veya farkı alınan doğal sayılarla çarparken, bu rasyonel sayı ile toplanan veya farkı alınan doğal sayılar ayrı ayrı çarpılır ve bu çarpımlar toplanır veya çıkarılır. Yapılan bu işleme rasyonel sayılarla çarpma işleminin toplama veya çıkarma işlemi üzerine dağılma özelliği denir.
- \dfrac{a}{b} × (\dfrac{c}{d} + \dfrac{e}{f} ) = \dfrac{a}{b} × \dfrac{c}{d} + \dfrac{a}{b} × \dfrac{e}{f} rasyonel sayılarla çarpma işleminin toplama işlemi üzerine dağılma özelliği
- \dfrac{a}{b} × (\dfrac{c}{d} – \dfrac{e}{f} ) = \dfrac{a}{b} × \dfrac{c}{d} – \dfrac{a}{b} × \dfrac{e}{f} rasyonel sayılarla çarpma işleminin çıkarma işlemi üzerine dağılma özelliği
Örneğin;
\dfrac{1}{4} × (\dfrac{2}{5} + \dfrac{1}{5} ) = \dfrac{1}{4} × \dfrac{2}{5} + \dfrac{1}{4} × \dfrac{1}{5}
\dfrac{1}{4} × \dfrac{3}{5} = \dfrac{2}{20} + \dfrac{1}{20}
\dfrac{3}{20} = \dfrac{3}{20}
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Rasyonel Sayılarla Toplama Ve Çıkarma İşlemi | Rasyonel Sayılarla Çok Adımlı İşlemler |

