Rasyonel Sayılar ve Sayı Doğrusunda Gösterme
Kazanım: Rasyonel sayıları tanır ve sayı doğrusunda gösterir.
Bu konuda neler öğreneceğiz :
RASYONEL SAYILAR
Sayı doğrusunda iki tam sayı arasında sonsuz tane sayı bulunmaktadır.
Örneğin; aşağıdaki sayı doğrusunda 3 ve 4 arasında sonsuz tane nokta (sayı) varıdır.

3 ve 4 arasında sonsuz tane nokta olmadığını düşünüyorsanız 3 ve 4 arasını genişlettiğinizde daha fazla sayıda nokta oluşturursunuz. Bu işlemi sonsuz genişliğe uzattığımızı varsaydığımızda sonsuz noktaya ulaşmış oluruz.
Önceki senelerde bu noktaların varlığından haberimiz vardı ama noktaların hangi sayı grubuna ait olduğunu bilmiyorduk.
Bu noktaları tanımlayacak olursak sayı doğrusunda bulunan tüm noktalar rasyonel sayıdır.

Bilgi: a bir tam sayı ve b sıfırdan farklı bir tam sayı olmak üzere \dfrac{a}{b} şeklinde yazılabilen sayılara rasyonel sayılar denir. Kısaca iki tam sayının oranı olarak yazabildiğimiz sayılara rasyonel sayılar denir. Rasyonel sayılar Q sembolü ile gösterilir.
Bir sayının rasyonel sayı olabilmesi için \dfrac{a}{b} şeklinde (b sıfırdan farklı bir tam sayı olmak şartıyla) yani kesirli olarak ifade edilebilmesi lazım.
Örneğin; \dfrac{3}{7} , \dfrac{-4}{9} , 4 \dfrac{2}{3} , – \dfrac{5}{7} , \dfrac{1}{5} ,……. gibi \dfrac{a}{b} şeklinde yazılabilen sayılar rasyonel sayılardır.
Not: Sıfır hariç bir sayının sıfıra bölümü tanımsızdır.
Örneğin;
\dfrac{5}{0} , \dfrac{-4}{0} , \dfrac{11}{0} gibi ifadeler tanımsızdır. ve bu ifadeler rasyonel sayı değildir.
Not: Sıfırın sıfıra bölümü belirsizdir.
Örneğin;
\dfrac{0}{0} belirsizdir ve bu ifade rasyonel sayı değildir.
Not: Sıfırdan büyük rasyonel sayılar pozitif rasyonel sayılar , sıfırdan küçük rasyonel sayılar negatif rasyonel sayılar , sıfır ise ne pozitif nede negatif rasyonel sayıdır.
➡️ \dfrac{2}{7} , + \dfrac{5}{9} , \dfrac{11}{5} , \dfrac{13}{2} ,………. gibi sayılar pozitif rasyonel sayılardır.
➡️ – \dfrac{2}{5} , ,- \dfrac{6}{5} , – \dfrac{12}{5} , – \dfrac{8}{2} ,………. gibi sayılar negatif rasyonel sayılardır.
➡️ \dfrac{0}{9} , \dfrac{0}{11} , \dfrac{0}{5} , 0,………. gibi sayılar ne pozitif nede negatif rasyonel sayıdır.
Not: Negatif bir rasyonel sayının eksi işareti payın önünde de bulunabilir, kesir çizgisinin önünde de bulunabilir, paydanın önünde de bulunabilir. Hepsi aynı sayıyı gösterir.
Örneğin;
– \dfrac{3}{8} rasyonel sayısı , \dfrac{-3}{8} rasyonel sayısı ve \dfrac{3}{-8} rasyonel sayısı birbirine eşittir.
– \dfrac{3}{8} = \dfrac{-3}{8} = \dfrac{3}{-8}
Yani ”➖” işaretinin pay ,payda veya kesir çizgisi hizasında olmasının bir önemi yoktur.
Not: Her tam sayı, iki tam sayının oranı şeklinde ( \dfrac{a}{b} ) yazılabilir. Bu yüzden bütün tam sayılar aynı zamanda rasyonel sayıdır.
Örneğin;
➡️ 7 tam sayısı \dfrac{7}{1} şeklinde yazılabildiği için 7 tam sayısı rasyonel sayıdır.
➡️ -9 tam sayısı \dfrac{-9}{1} şeklinde yazılabildiği için -9 tam sayısı rasyonel sayıdır.
➡️ 13 tam sayısı \dfrac{13}{1} şeklinde yazılabildiği için 13 tam sayısı rasyonel sayıdır.

Not: Ondalıklı sayılar \dfrac{a}{b} şeklinde yazılabildiği için rasyonel sayıdır.
Örneğin;
➡️ 2,3 ondalıklı sayısı \dfrac{23}{10} şeklinde yazılabildiği için 2,3 ondalık sayısı rasyonel sayıdır.
➡️ -0,6 ondalıklı sayısı \dfrac{-6}{10} şeklinde yazılabildiği için -0,6 ondalık sayısı rasyonel sayıdır.
➡️ 2,7 ondalıklı sayısı \dfrac{27}{10} şeklinde yazılabildiği için 2,7 ondalık sayısı rasyonel sayıdır.
Konuyu pekiştirmek için aşağıdaki etkinliği çözünüz.
Rasyonel Sayıları Sayı Doğrusunda Gösterme
Sayı doğrusunda tam sayıları yerini göstermeyi önceki senelerde öğrenmiştik. Şimdi ise tam sayı olmayan rasyonel sayıları da sayı doğrusunda nasıl göstereceğimizi öğreneniz. Rasyonel sayıları sayı doğrusunda göstermeyi tam kısmının olup olmamasına göre iki ayrı başlıkta anlatacağız. Şimdi bu iki başlığı ayrı ayrı anlatalım.
Tam kısmı olmayan rasyonel sayıları sayı doğrusunda gösterme:
Tam kısmı olmayan rasyonel sayılar \dfrac{3}{7} , \dfrac{-7}{3} , \dfrac{11}{5} , – \dfrac{13}{2} şeklindeki basit kesir veya bileşik kesirlerdir.
Tam kısmı olmayan rasyonel sayıları sayı doğrusunda gösterirken aşağıdaki adımları takip ederiz.
- Ardışık tam sayıların arasını rasyonel sayının paydası kadar eş aralığa böleriz.
- Sayı doğrusunda sıfırdan başlarız.
- Rasyonel sayı pozitif ise sayı doğrusunda sağa doğru , negatif ise sayı doğrusunda sola doğru pay kadar ilerleriz.
Örneğin;
\dfrac{13}{4} rasyonel sayısını yukarıdaki adımları takip ederek sayı doğrusunda gösterelim.
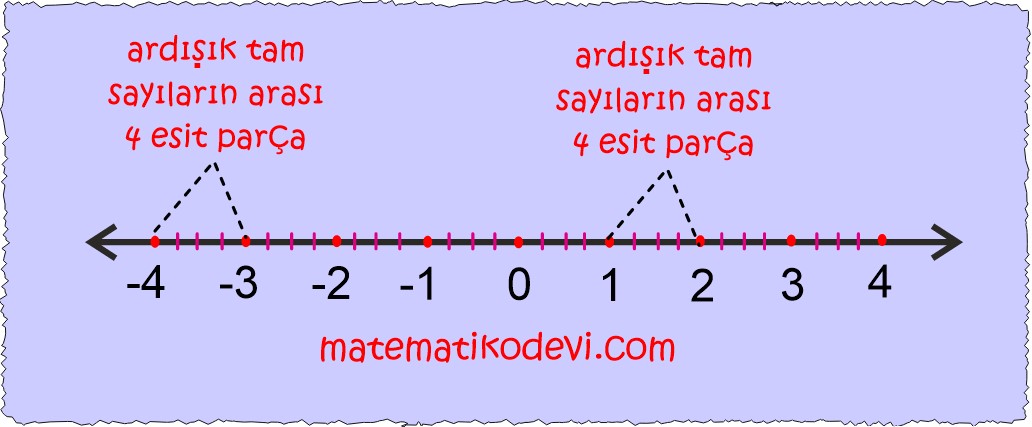
- Ardışık tam sayıların arasını rasyonel sayının paydası kadar eş aralığa böleriz.
Payda 4 olduğu tam sayıların arasını 4 eşit parçaya ayıralım.
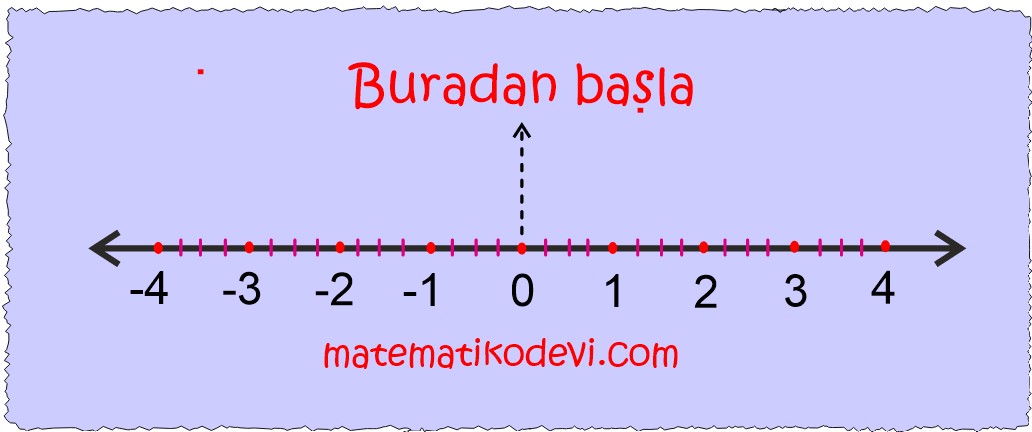
- Sayı doğrusunda sıfırdan başlarız.
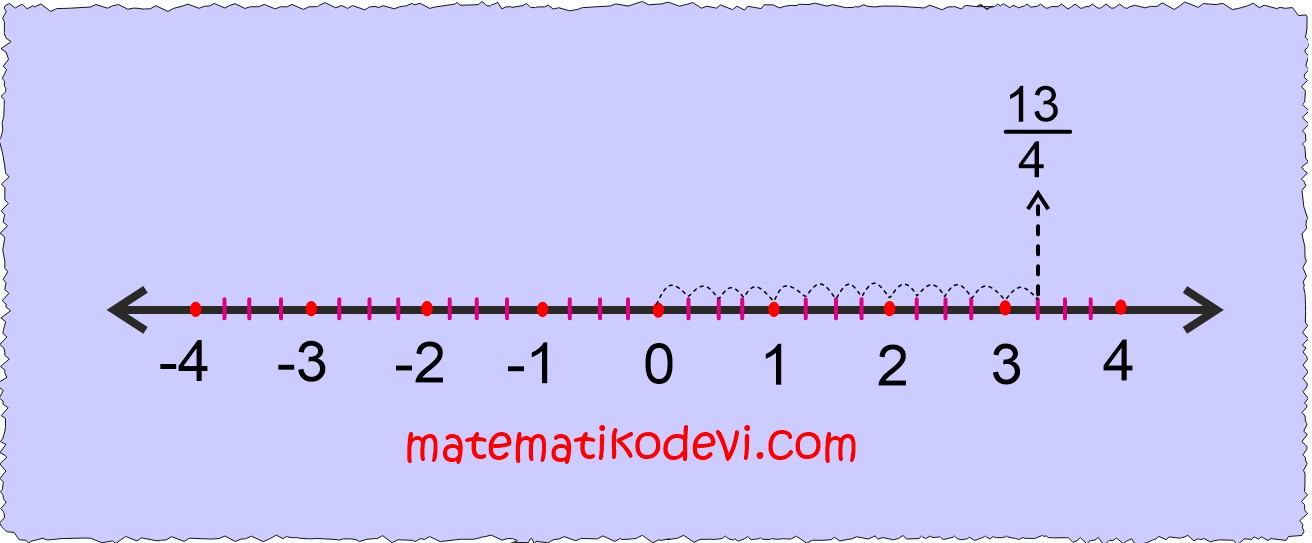
- Rasyonel sayı pozitif ise sayı doğrusunda sağa doğru , negatif ise sayı doğrusunda sola doğru pay kadar ilerleriz.
Pay 13 ve rasyonel sayı pozitif olduğu için sıfırdan başlayıp sağa doğru 13 aralık ilerleriz.
Konuyu pekiştirmek için aşağıdaki etkinliği yapabilirsiniz.
Tam kısmı olan rasyonel sayıyı sayı doğrusunda gösterme:
Tam kısmı olan rasyonel sayılar 3 \dfrac{2}{5} , 5 \dfrac{2}{3} , -4 \dfrac{1}{6} , – \dfrac{4}{7} şeklindeki tam kısımdan oluşan kesirlerdir.
Tam kısmı olan rasyonel sayıları sayı doğrusunda gösterirken aşağıdaki adımları takip ederiz.
- Ardışık tam sayıların arasını rasyonel sayının paydası kadar eş aralığa böleriz.
- Sayı doğrusunda rasyonel sayının tam kısmından başlarız.
- Rasyonel sayı pozitif ise sayı doğrusunda sağa doğru , negatif ise sayı doğrusunda sola doğru pay kadar ilerleriz.
Örneğin;
-2 \dfrac{3}{4} rasyonel sayısını yukarıdaki adımları takip ederek sayı doğrusunda gösterelim.
- Ardışık tam sayıların arasını rasyonel sayının paydası kadar eş aralığa böleriz.
Payda 4 olduğu tam sayıların arasını 4 eşit parçaya ayıralım.

- Sayı doğrusunda rasyonel sayının tam kısmından başlarız.

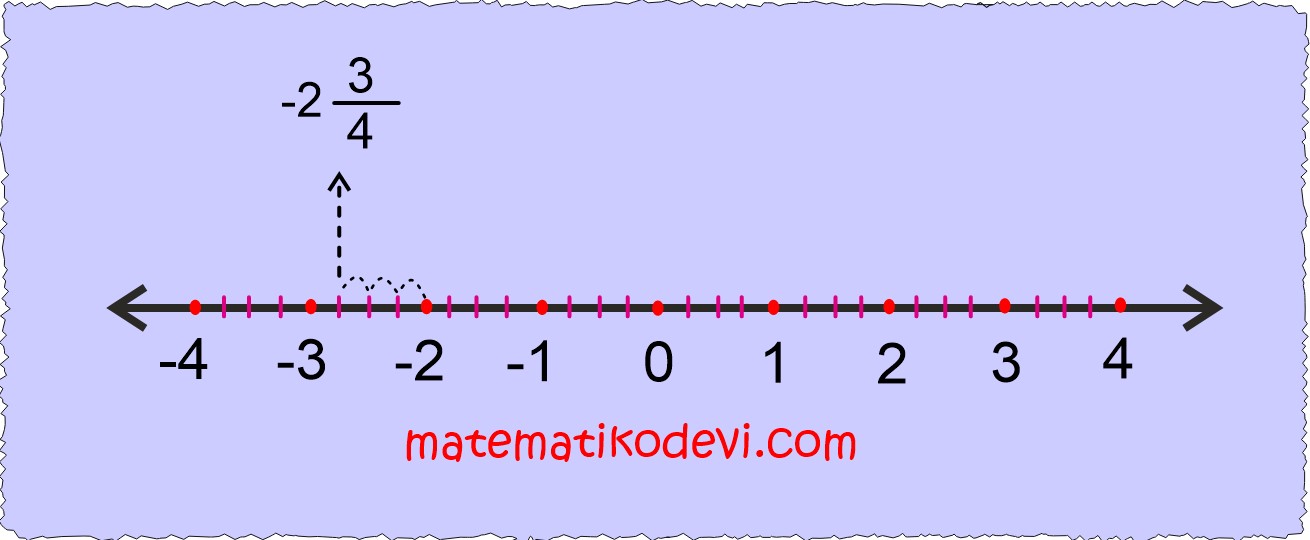
- Rasyonel sayı pozitif ise sayı doğrusunda sağa doğru , negatif ise sayı doğrusunda sola doğru pay kadar ilerleriz.
Pay 3 ve rasyonel sayı negatif olduğu için -2’den başlayıp sola doğru 3 aralık ilerleriz.
7.Sınıf 2.Konuya bu başlık ile başladık. Konu devamı için aşağıda ki bağlantıları kullanabilirsiniz. Konu ile alakalı sorularınız olursa yorumda belirtebilirsiniz. Bu konuyu pekiştirmek için 7. Sınıf arşiv, online test ve etkinlik sayfalarını kullanabilirsiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Rasyonel Sayıların Ondalık Gösterimi Ve Devirli Ondalık Sayılar |

