Özdeşlikler Konu Anlatımı-8.Sınıf
Kazanım: Özdeşlikleri modellerle açıklar.
Bu konuda neler öğreneceğiz :
Özdeşlik Nedir?
Bilgi: Bilinmeyenine verilen her değer için doğru olan açık eşitliklere özdeşlik denir.
Verilen eşitlik sadece bir kaç sayı değeri için eşitliği sağlıyor ise özdeşlik değildir(denklem) denir.Verilen eşitlik tüm gerçek sayılar için eşitliği sağlıyor ise özdeşlik denir.
Örneğin;
✅ 4x-7=2x+5 eşitliği özdeşlik mi özdeşlik değil mi bulalım.
➡ x=6 için eşitlik sağlanır mı bakalım
4·6-7=2·6+5
24-7=12+5
7=7
➡ x=2 için eşitlik sağlanır mı bakalım.
4·2-7=2·2+5
8-7=4+5
1≠9
➡ Yukarıda verdiğimiz iki değerden biri için eşitlik sağlanırken diğeri için eşitlik sağlanmadı.Bu yüzden 4x-7=2x+5 eşitliği özdeşlik değildir.(denklem)
✅ 3x-9=3(x-3) eşitliği özdeşlik mi özdeşlik değil mi bulalım.
➡ x=1 için eşitlik sağlanır mı bakalım
3·1-9=3·(1-3)
3-9=3·(-2)
-6=-6
➡ x=2 için eşitlik sağlanır mı bakalım.
3·2-9=3·(2-3)
6-9=3·(-1)
-3=-3
➡ Yukarıda verdiğimiz iki değerden ikisi içinde eşitlik sağlanır Başka değer vermeye devam etsek de eşitlik sağlanır.Bu yüzden 3x-9=3(x-3) eşitliği özdeşliktir.
Bilgi: Verilen cebirsel ifadenin özdeşlik olup olmadığını anlamak için eşitliğin sağındaki cebirsel ifade ile eşitliğin solundaki cebirsel ifadenin aynı olup olmadığına bakarız Eşitliğin her iki tarafı da aynı çıkıyor ise özdeşliktir denir.

Örnek: 30a-18=6·(5a-3) eşitliği özdeşlik mi bakalım.
➡ Eşitliğin sağ tarafındaki dağılma özelliğini yapalım
6·(5a-3)
6·5a – 6·3
30a-18 eşitliğin sol tarafındaki ifadeye eşit çıktı
➡ Eşitliğin sol tarafı sağ tarafına eşit çıktığı için 30a-18=6·(5a-3) eşitliği özdeşliktir denir.
Önemli Özdeşlikler
Şimdi sorularda çok sık karşımıza çıkan önemli özdeşlikleri inceleyelim
Tam Kare Özdeşliği
Tam kare özdeşliği iki terimin toplamının karesi (x+y)2 ve iki terimin farkının karesi (x-y)2 olmak üzere iki farklı şekilde ifade edilmektedir.
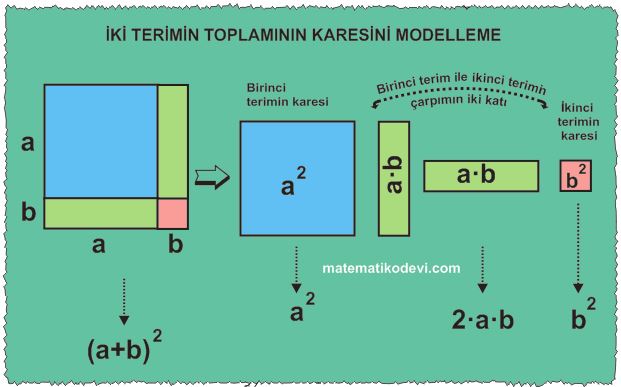
İki Terimin Toplamının Karesi
Bilgi: İki terimin toplamının karesi, bu iki terimin kareleri ile bu iki terimin çarpımının iki katının toplamına eşittir.
✅ (a + b)2 = a2 + 2ab + b2
✅ Bu durumu birinci terimin karesi , ikinci terimin karesi ve birinci terim ile ikinci terimin çarpımının iki katının toplamı olarak da açıklayabiliriz.

Örnek: Aşağıda verilen özdeşliklerin açılımını yapalım.
✅ (a+3)2 = ?
➡ Birinci terimin karesi
a2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2·a·3
6a
➡ İkinci terimin karesi
32
9
➡ Birinci terimin karesi , ikinci terimin karesi ve birinci terim ile ikinci terimin çarpımının iki katının toplamı
a2 + 6a + 9
✅ (2b+4)2 = ?
➡ Birinci terimin karesi
(2b)2
4b2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2·b·4
8b
➡ İkinci terimin karesi
42
16
➡ Birinci terimin karesi , ikinci terimin karesi ve birinci terim ile ikinci terimin çarpımının iki katının toplamı
4b2 + 8b + 16
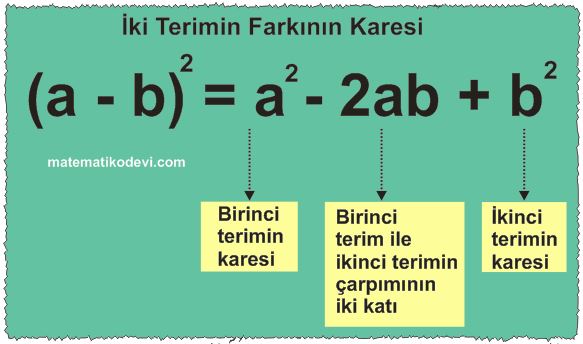
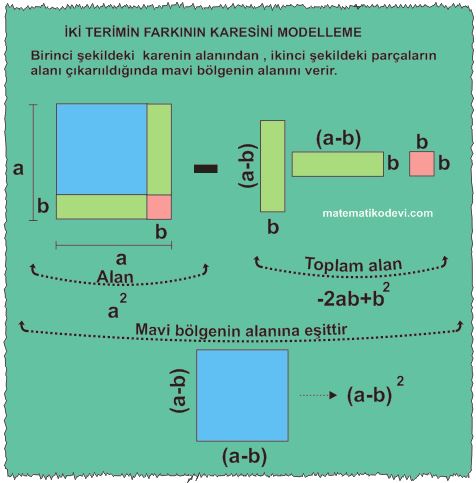
İki Terimin Farkının Karesi
Bilgi: İki terimin farkının karesi, bu iki terimin kareleri toplamından bu iki terimin çarpımının iki katının çıkarılmasına eşittir.
✅ (a + b)2 = a2 – 2ab + b2
✅ Bu durumu birinci terimin ve ikinci terimin karesinin toplamından ve birinci terim ile ikinci terimin çarpımının iki katının farkı olarak da açıklayabiliriz.
Örnek: Aşağıda verilen özdeşliklerin açılımını yapalım.
✅ (a-5)2 = ?
➡ Birinci terimin karesi
a2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2·a·5
10a
➡ İkinci terimin karesi
52
25
➡ Birinci terimin ve ikinci terimin karelerinin toplamından ve birinci terim ile ikinci terimin çarpımının iki katının çıkarılması
a2 – 10a + 25
✅ (5b-6)2 = ?
➡ Birinci terimin karesi
(5b)2
25b2
➡ Birinci terim ile ikinci terimin çarpımının iki katı
2·5b·6
60b
➡ İkinci terimin karesi
62
36
➡ Birinci terimin ve ikinci terimin karelerinin toplamından ve birinci terim ile ikinci terimin çarpımının iki katının çıkarılması
25b2 – 60b + 36
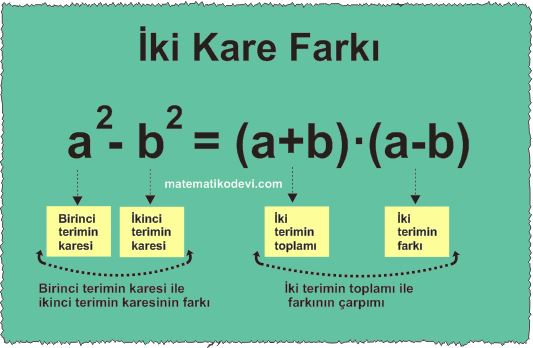
İki Kare Farkı Özdeşliği
Bilgi: İki terimin karelerinin farkı, bu iki terimin toplamı ile farkının çarpımına eşittir.
✅ a2 − b2 = (a − b) . (a + b)
Örnek: Aşağıda verilen ifadelerin özdeşliklerini yazınız.
✅ x2 – 9y2 = ?
➡ Birinci terim x’in karesi x2 = x2
➡ İkinci terim 3y’nin karesi (3y)2 =9y2
➡ Birinci terim ile ikinci terimin kareleri farkı x2 – 9y2
➡ İki terimin toplamı ile farkının çarpımı (x+3y)·(x-3y)
x2 – 9y2 = (x+3y)·(x-3y)
✅ 25 – 16a2 = ?
➡ Birinci terim 3’ün karesi 32 = 9
➡ İkinci terim 4a’nın karesi (4a)2 =16a2
➡ Birinci terim ile ikinci terimin kareleri farkı 9 – 16a2
➡ İki terimin toplamı ile farkının çarpımı (3+4a)·(3-4a)
9 – 16a2 = (3+4a)·(3-4a)
✅ (3x+5a)·(3x-5a) = ?
➡ Birinci terimin karesi (3x)2 = 9x2
➡ İkinci terimin karesi (5a)2 =25a2
➡ Birinci terim ile ikinci terimin kareleri farkı 9x2 – 25a2
(3x+5a)·(3x-5a) = 9x2 – 25a2
İki Kare Farkı Özdeşliği Modellemesi
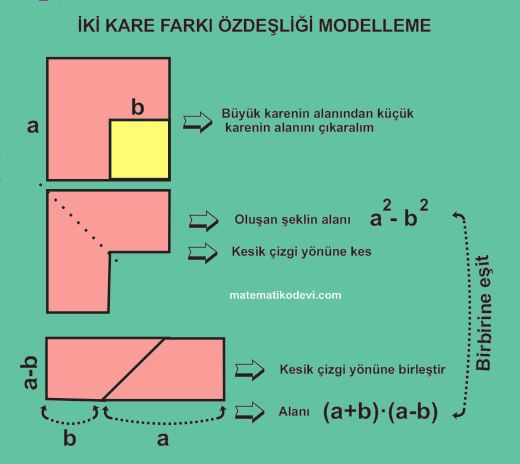
Özdeşlikler Eşleştirme Testi
Özdeşlikler 8.Sınıf Test
Yeni Nesil Soru
🎥 Bir Soru Bir Video 🎥
Soru: Slot makinesi oyununu cebirsel ifadelere uyarlayan Sena oyunu aşağıdaki gibi tasarlamıştır.
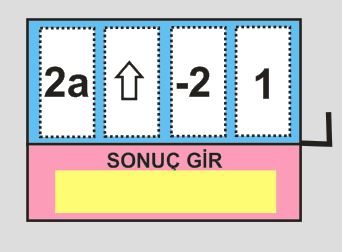
Yukarıda verilen görseldeki ifadelere göre (2a+-2)1 = 2a-2
Sena ”SONUÇ GİR” ekranına 2a-2 yazdığında oyunu kazanır,başka bir ifade girdiğinde oyunu kaybeder.
Slot makinesinin kolunu iki defa çeviren Sena birincisinde oyunu kaybetmiş,ikincisinde oyunu kazanmış ve aşağıdaki görselde 1. ve 2. çevirme sonucu oluşan görüntüler verilmiştir.
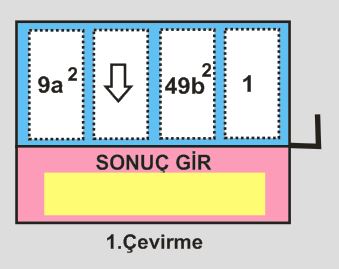
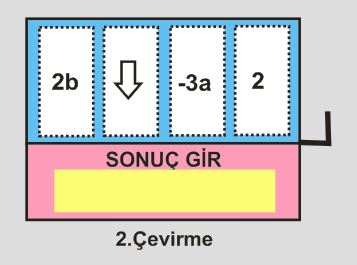
Buna göre Sena 1.çevirme ve 2.çevirme sonucunda ”SONUÇ GİR” ekranına aşağıdakilerden hangisini girmiş olabilir?
| 1.Çevirme | 2.Çevirme |
| A) (3a+b)·(3a-b) | 4b2 +12ab +9b2 |
| B) (3a+b)·(3a-b) | 4b2 – 12ab +9b2 |
| C) (3a+7b)·(3a-7b) | 4b2 +12ab +9b2 |
| D) (3a+7b)·(3a-7b) | 4b2 – 12ab +9b2 |
Çözüm:
Konu anlatımının devamı için tıklayınız..

