Koninin Temel Elemanları ve Açınımı Konu Anlatımı

Koninin Temel Elemanları ve Açınımı kazanımı ;

[alert color=”warning”]Kazanım: Dik koniyi tanır, temel elemanlarını belirler, inşa eder ve açınımını çizer. [/alert]

DİK DAİRESEL KONİ

[alert color=”primary”]Bilgi: Tabanı daire olan piramide koni denir. [/alert]

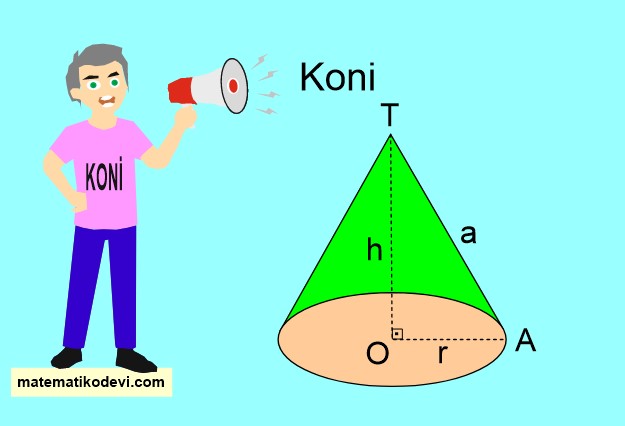
Koni tabanı daire ve yan yüzeyi daire diliminden oluşmaktadır.

Koninin Temel Elemanları

Koninin Temel elemanları;

a. tabanı,
b. tepe noktası,
c. ekseni (cisim yüksekliği),
d. ana doğrusu (doğuran),
e. yanal yüzeyi,
f. merkez açısıdır.

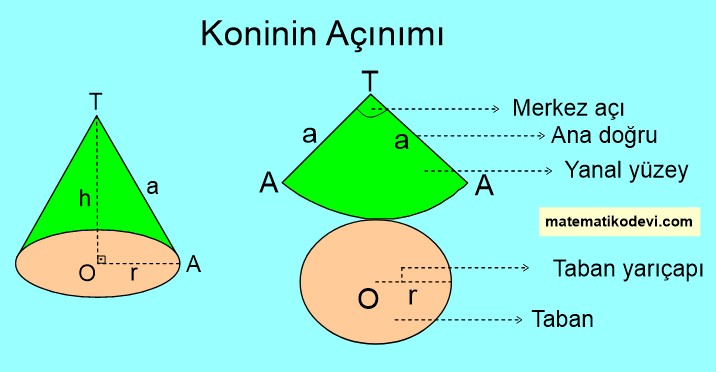
🤓 Koninin yanal yüzeyi yarıçapı a birim olan bir daire dilimidir. Daire diliminin açısı bu daire diliminin merkez açısıdır.

Yukarıda görselde verilen koninin;

Taban	Tepe noktası	Eksen	Ana doğru
O merkezli r yarıçaplı daire	T noktası	[TO]	[TA]

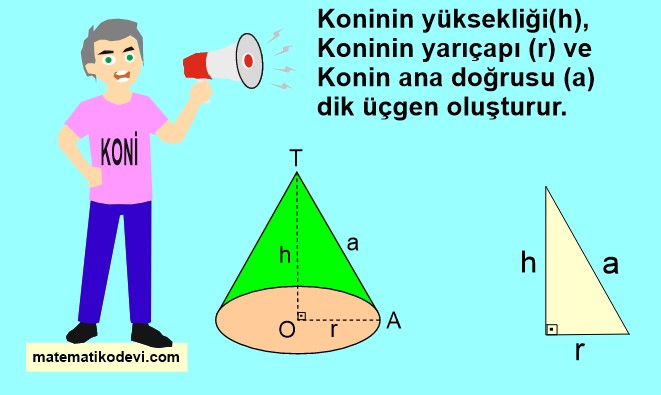
🤓 Dik dairesel konide h cisim yüksekliği, a ana doğru olmak üzere ve r taban yarıçapı olmak üzere;

📌 h²+ r² = a²

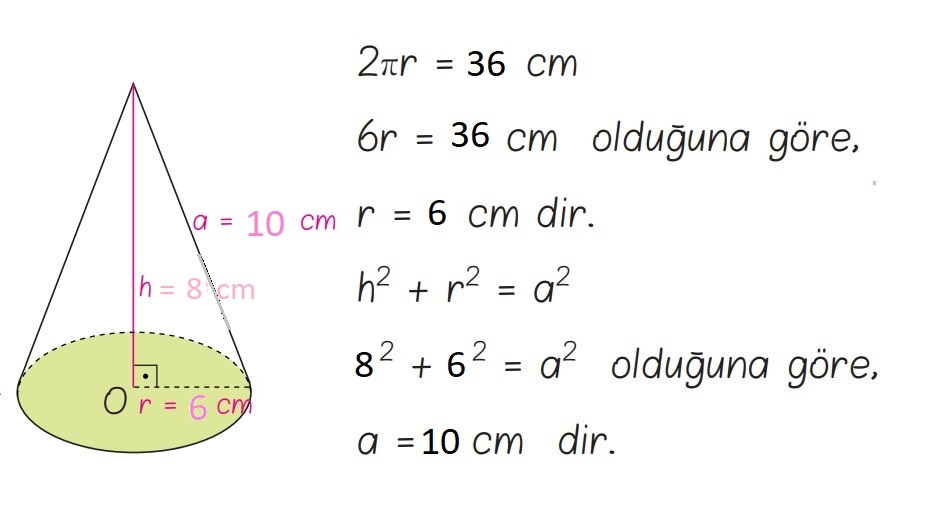
Örnek: Bir dik koninin taban çevresi 36 cm, yüksekliği 8 cm olduğuna göre, ana doğrusunun uzunluğunun kaç cm olduğunu bulalım. (π = 3 alınız.)

Çözüm:

🤓 Koninin açınımında daire diliminin yay uzunluğu , Tabandaki dairenin çevresine eşittir.

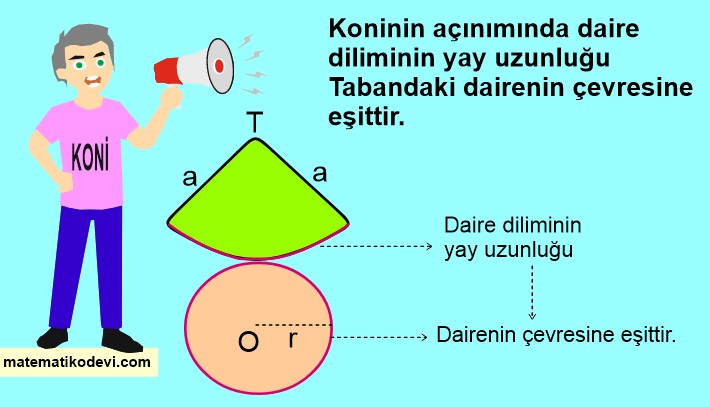
Koninin Ana doğrusu ile Taban yarıçap ilişkisi

🤓 Konini daire diliminin yay uzunluğunun , taban çevresine eşitliğinden yola çıkarak koninin taban yarıçapı ile ana doğrusu arasındaki ilişkiyi inceleyelim.

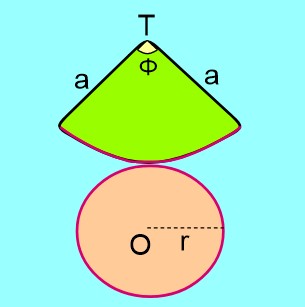
Yukarıdaki koniye göre adım adım ana doğru , merkez açı ve taban yarıçapı ilişkisini ile inceleyelim.

1.adım: Bir koninin açınımı üzerinde r, a ve Φ değerlerini işaretleyelim.

2.adım: T merkezli a yarıçaplı daire diliminin yay uzunluğunu bulalım.

 Daire diliminin yay uzunluğu= \dfrac{Φ}{360°} ·2πa

3.adım: O merkezli r yarıçaplı tabandaki dairenin çevresini bulalım. Ç(O, r) = 2πr

4.adım: Açınımı yapılmış koninin, kapanabilmesi için daire diliminin yay uzunluğu ile tabandaki dairenin çevre uzunluğu eşit olmalıdır.

2πr = \dfrac{Φ}{360°} ·2πa

5.adım: Eşitliğin her iki tarafındaki 2π terimleri sadeleşir.

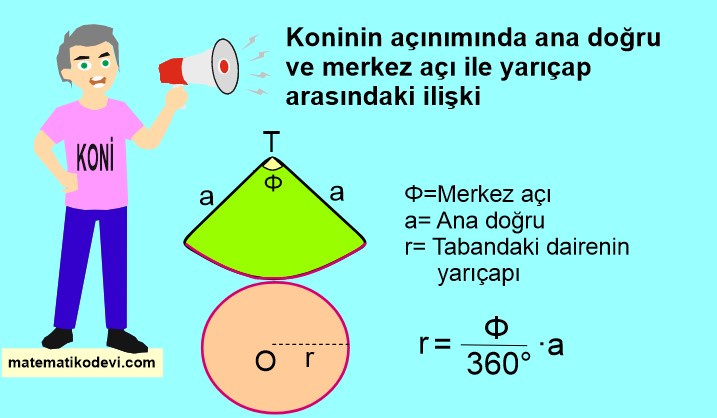
r = \dfrac{Φ}{360°} ·a

☝️ Koninin ana doğru , merkez açı ve taban yarıçapı ile ilişkisi ☝️

Örnek:

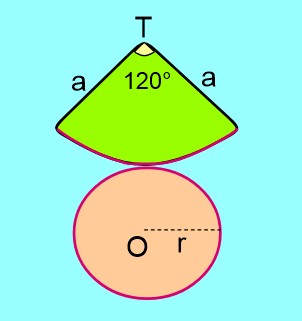
Yukarıdaki koninin ana doğrusu 42 cm olduğuna göre taban çevresinin kaç cm olduğunu bulalım.(π=3 alınız)

Çözüm:

👉 Tabandaki dairenin yarıçapını bulalım.

r = \dfrac{Φ}{360°} ·a

r = \dfrac{120°}{360°} ·42

r=14 cm

👉 tabandaki dairenin çevresini bulalım.

Çevre = 2πr

Çevre=2·3·14

Çevre=84 cm

Konu Tekrarı Linki : https://www.matematikodevi.com/geometrik-cisimler-8-sinif-konu-anlatimi/