Kesirlerde Bölme İşlemi Konu Anlatımı
Kazanım: İki kesrin bölme işlemini yapar ve anlamlandırır.
Bu konuda neler öğreneceğiz :
Kesirlerde Bölme İşlemi
İki Kesri Bölme
Bir kesri başka bir kesre bölmek demek kesrinde kaç tane bölen kesir olduğunu bulmak demektir.
Örneğin \dfrac{3}{4} ÷ \dfrac{1}{8} bölme işlemi \dfrac{3}{4} kesrinin içinde kaç tane \dfrac{1}{8} kesri olduğunu bulma işlemidir. Aşağıdaki görselde \dfrac{3}{4} kesrinin içinde kaç tane \dfrac{1}{8} kesri olduğu gösterilmiştir.
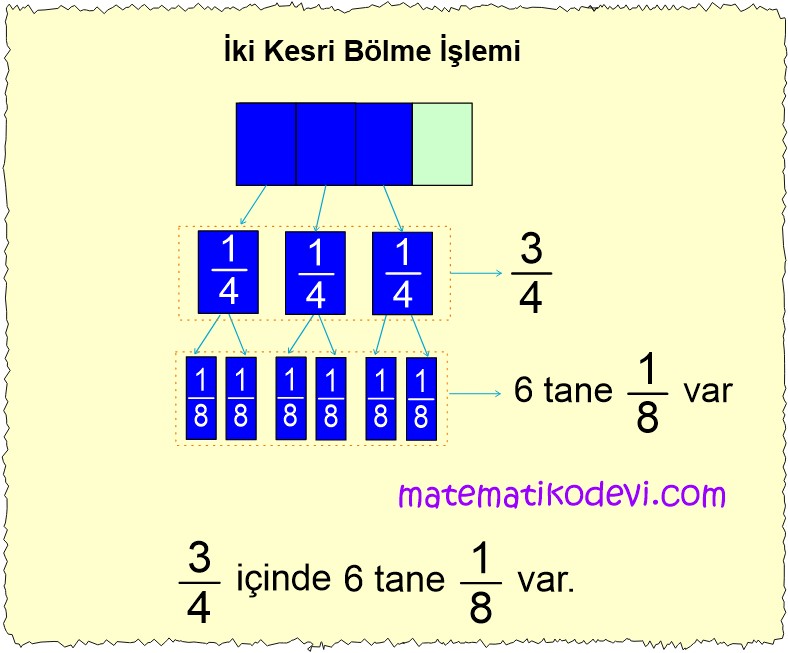
Görseli incelediğimizde \dfrac{3}{4} kesrinin içinde 6 tane \dfrac{1}{8} kesri olduğunu görürüz.
Bu durumu \dfrac{3}{4} ÷ \dfrac{1}{8} = 6 olarak gösteririz.
Bilgi: İki kesri bölerken birinci kesir (yani bölünen) aynen yazılır, ikinci kesir (yani bölen) ters çevrilerek çarpılır.
Örneğin;
\dfrac{3}{5} ÷ \dfrac{2}{7} bölme işlemini yapalım.
➡️ Birinci kesir aynen yazılır, ikinci kesir ters çevrilerek çarpılır.
\dfrac{3}{5} × \dfrac{7}{2}
\dfrac{3×7}{5×2}
\dfrac{21}{10}
\dfrac{3}{5} ÷ \dfrac{2}{7} bölme işleminin sonucu \dfrac{21}{10} olur.
Bilgi: Kesirlerde bölme işlemini yaptıktan sonra sadeleştirme varsa sadeleştirme yapılır.
✅ İstersek sadeleştirmeyi bölmeyi çarpmaya dönüştürdükten sonra (çarpmayı yapmadan önce) yapabiliriz. Bu şekilde sadeleştirme yapmak daha kolaydır.
Sadeleştirme konusunu hatırlamak için tıklayınız.
Örneğin;
\dfrac{12}{5} ÷ \dfrac{3}{10} bölme işlemini yapalım.
➡️ Birinci kesir aynen yazılır, ikinci kesir ters çevrilerek çarpılır.
\dfrac{12}{5} × \dfrac{10}{3}
\dfrac{12×10}{5×3}
\dfrac{120}{15}
🤓 \dfrac{120}{15} kesrinin Pay ve paydası 15 ile bölündüğü için
\dfrac{120}{15} kesrini 15 ile sadeleştirebiliriz.
\dfrac{120÷15}{15÷15}
\dfrac{8}{1} = 8
🤓 Sadeleştirmeyi bölmeyi çarpmaya dönüştürdükten sonra (çarpmayı yapmadan önce) yapabiliriz.
\dfrac{12}{5} × \dfrac{10}{3}
İstersek bu adımda çarpma yapmadan önce sadeleştirme yapabiliriz.
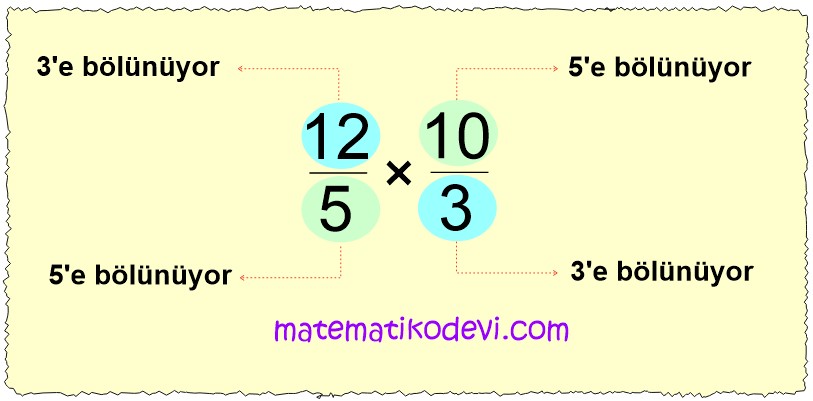
\dfrac{12÷3}{5÷5} × \dfrac{10÷5}{3÷3}
\dfrac{4}{1} × \dfrac{2}{1}
\dfrac{4×2}{1×1}
\dfrac{8}{1} = 8
Bilgi: Bölme işlemi yaparken tam sayılı kesir varsa bileşik kesre çevrilir.
Örneğin;
2 \dfrac{1}{2} ÷1 \dfrac{2}{5} bölme işlemini yapalım.
➡️ Tam sayılı kesri bileşik kesre çeviririz.
2 \dfrac{1}{2} = \dfrac{5}{2}
1 \dfrac{2}{5} = \dfrac{7}{5}
➡️ Bileşik kesre çevirdikten sonra birinci kesir aynen yazılır, ikinci kesir ters çevrilerek çarpılır.
\dfrac{5}{2} × \dfrac{5}{7}
\dfrac{5×5}{2×7}
\dfrac{25}{14}
Bilgi: İki kesri birbirine bölerken kesirlerin paydalarını eşitleyip sonra paylarını oran olarak yazabiliriz.
Örneğin;
\dfrac{5}{6} ÷ \dfrac{4}{9} bölme işlemini paydaları eşitleyerek yapalım.
➡️ Kesirlerin paydalarını eşitleyelim. (paydalar 18’de eşitlenir.)
\dfrac{5}{6} kesrini 3 ile genişletelim👉 \dfrac{5×3}{6×3} = \dfrac{15}{18}
\dfrac{4}{9} kesrini 2 ile genişletelim👉 \dfrac{4×2}{9×2} = \dfrac{8}{18}
➡️ Paydalarını eşitlediğimiz kesirlerin paylarını oran olarak yazalım.
\dfrac{15}{18} × \dfrac{8}{18}
\dfrac{15}{8} (Paylarının oranı)
\dfrac{5}{6} ÷ \dfrac{4}{9} bölme işleminin sonucu \dfrac{15}{8} olur.
Bilgi: Bir doğal sayı 1’den büyük bir kesre bölünürse sonuç bu sayıdan küçük olurken, 1’den küçük bir kesre bölünürse sonuç bu sayıdan büyük olur.
Örneğin;
8÷ \dfrac{9}{4} 👉 \dfrac{9}{4} 1’den büüyük olduğu için sonuç 8’den küçük olur.
8÷ \dfrac{2}{7} 👉 \dfrac{2}{7} 1’den küçük olduğu için sonuç 8’den büyük olur.
Kesirlerde Bölme İşlemi burada bitmiştir. Konu devamı için aşağıdaki bağlantıları kullanabilirsiniz.
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Doğal Sayıyı Kesre Bölme | Kesirlerde Yapılan İşlemlerin Sonucunu Tahmin Etme |

