Kareköklü Sayılarda Çarpma ve Bölme İşlemi Konu Anlatımı
Kazanım: Kareköklü ifadelerde çarpma ve bölme işlemlerini yapar.
Bu konuda neler öğreneceğiz :
Kareköklü Sayılarda Çarpma ve Bölme İşlemi Konu Anlatımı
Kareköklü Sayılarda Çarpma ve Bölme İşlemi konu anlatımı hakkında detaylı bilgiyi makalemizde bulabilirsiniz. Bu yazı ile ilgili sorularınızı yazı altından yorum yapabilirsiniz.
Kareköklü Sayılarda Çarpma İşlemi
Bilgi: Kareköklü sayılarla çarpma işlemi yapılırken varsa katsayılar çarpılır katsayı olarak yazılır. Kök içindeki sayılar çarpılır kök içinde yazılır.
✅ a√b×c√d=a×c√b×d
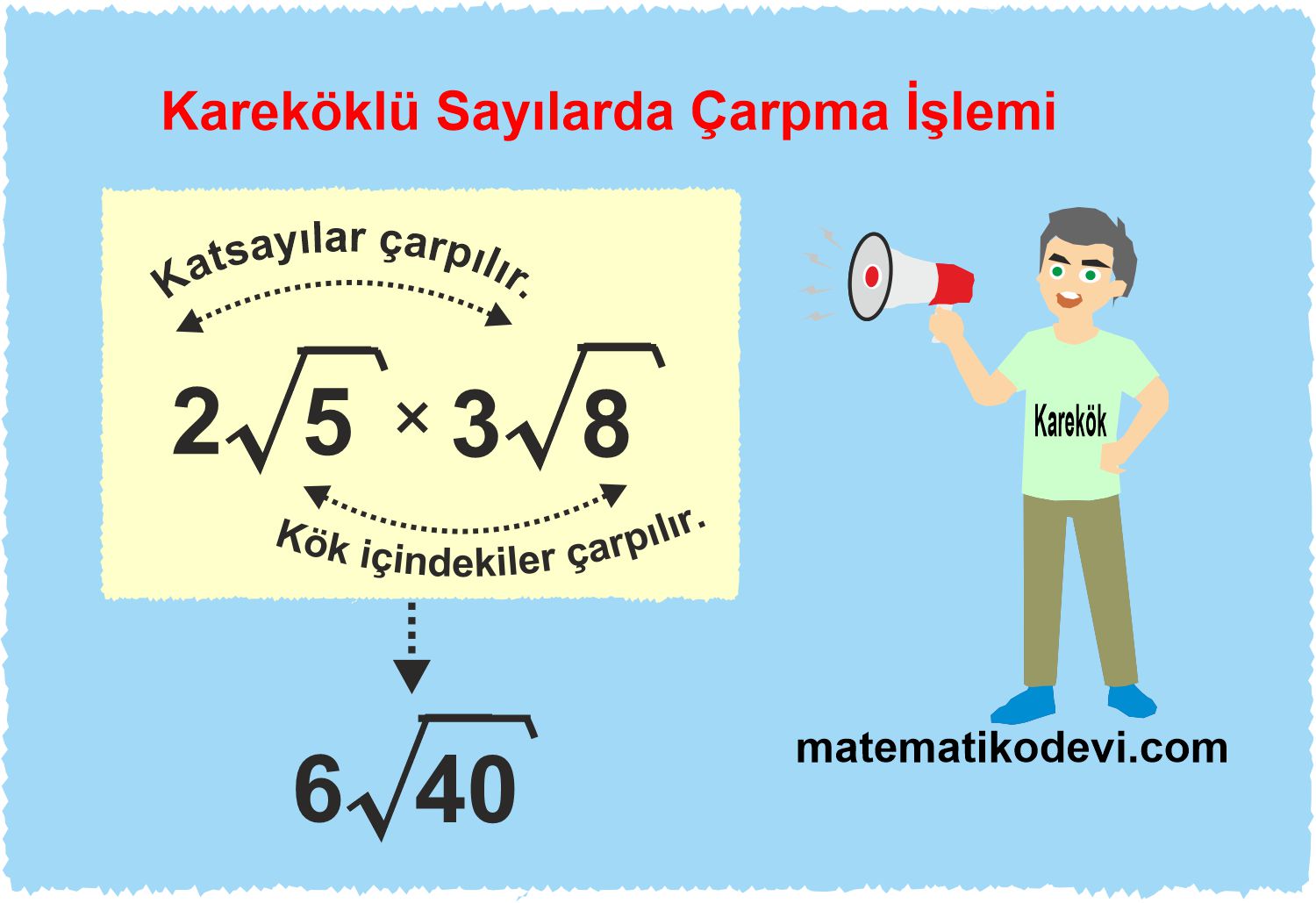
Not: Katsayısı olmayan kareköklü ifadelerin katsayısı 1 kabul edilir.
✅ √3 kareköklü sayısının katsayısı yoktur.Bu yüzden √3 sayısının katsayısı 1 olur.
Örnek: Aşağıda verilen çarpma işlemlerini yapalım.
➡ 6\sqrt {7} × 3\sqrt {2} =?
✅ Katsayıları çarpıp katsayı olarak , kök içindekileri çarpıp kök içinde yazarız
6×3\sqrt {7x2}
18\sqrt {14}
➡ 8\sqrt {3} × \sqrt {6} =?
✅ Katsayıları çarpıp katsayı olarak , kök içindekileri çarpıp kök içinde yazarız
8×1\sqrt {3x6}
🤓 Katsayısı olmayan kareköklü sayıların katsayısı 1 kabul edilir. 🤓
8\sqrt {18}
➡ 5\sqrt {7} × 4\sqrt {7} =?
✅ Katsayıları çarpıp katsayı olarak , kök içindekileri çarpıp kök içinde yazarız
5×4\sqrt {7x7}
20\sqrt {49}
🤓 Eğer kök içindeki sayı karekökden çıkyor ise kök dışına çıkarırız. 🤓
20\sqrt {49}
🤓 49 karekök dışına 7 olarak çıkar. 🤓
20×7=140
🤓 Karekökden çıkan sayı ile katsayı çarpılır. 🤓
Not: Karekök içinin aynı olduğu durumlarda çarpma işlemi yapılırken köklü sayı direk kök dışına çıkartılabilir.
✅ √b × √b = b
Örnek: Aşağıda verilen çarpma işlemlerini yapalım.
➡ \sqrt {6} × \sqrt {6} =?
✅ Karekök içi aynı ise köklü sayı direk kök dışına çıkartılabilir.
\sqrt {6x6}6
➡ 5\sqrt {3} × 4\sqrt {3} =?
✅ Karekök içi aynı ise köklü sayı direk kök dışına çıkartılabilir. Katsayılarla çarpılır.
5×4 \sqrt {3x3}
20 × 3 = 60
➡ 6\sqrt {10} × 2\sqrt {10} =?
✅ Karekök içi aynı ise köklü sayı direk kök dışına çıkartılabilir. Katsayılarla çarpılır.
6×2\sqrt {10x10}
12 × 10 = 120
Kareköklü Sayılarda Çarpma İşlemi – Etkinlik
Kareköklü Sayılarda Bölme İşlemi
Bilgi: Kareköklü sayılarda bölme işlemi yapılırken katsayılar bölünür katsayı kısmına , karekök içindeki sayılar bölünüp kök içine yazılır.
✅ a√b÷c√d=a÷c√b÷d
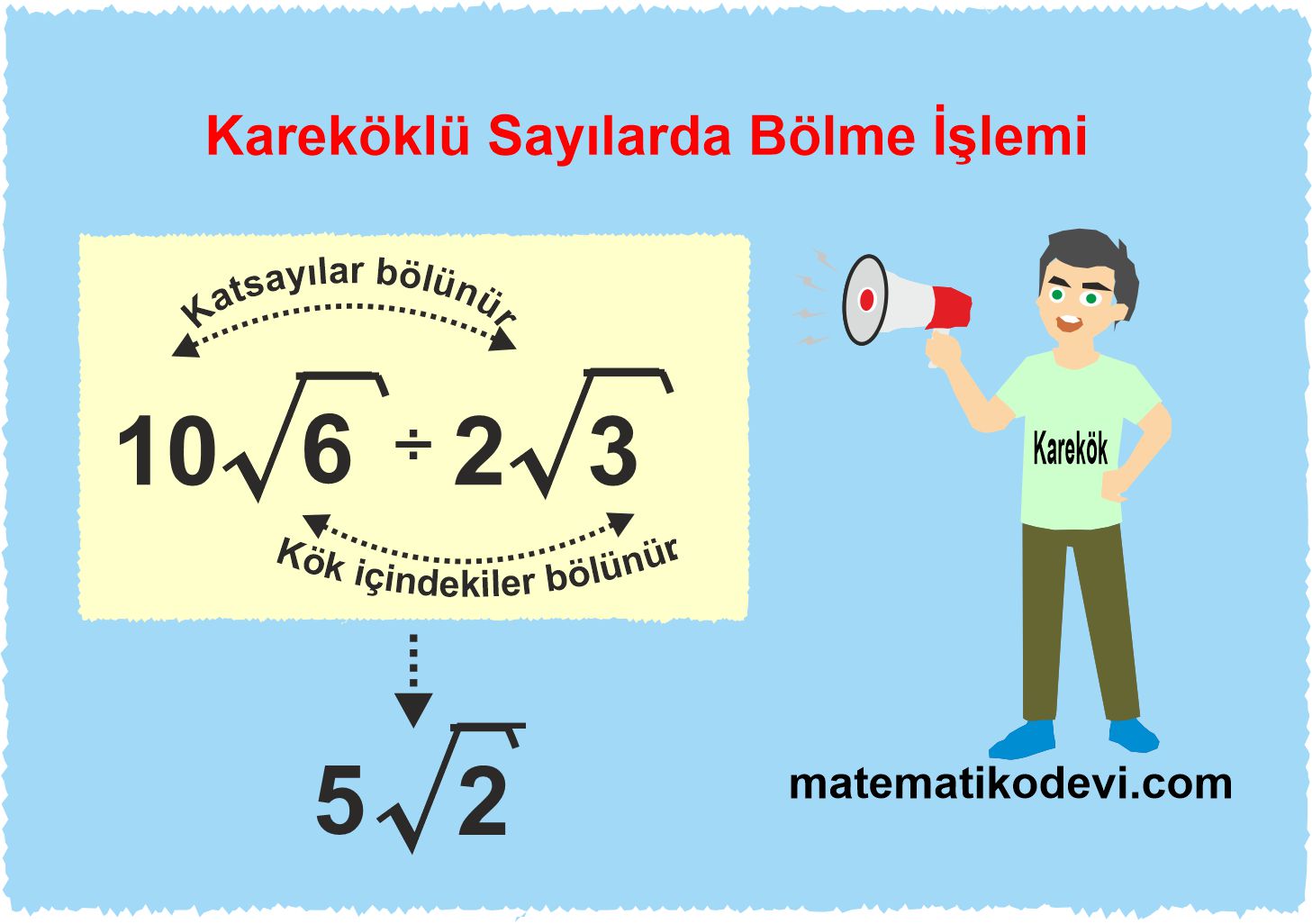
Örnek: Aşağıda verilen çarpma işlemlerini yapalım.
➡ 20\sqrt {21} ÷ 4\sqrt {7 } =?
✅ Katsayıları bölüp katsayı olarak , kök içindekileri bölüp kök içine yazarız
20÷4\sqrt {21÷7}
5\sqrt {3}
➡ 12\sqrt {40} ÷ \sqrt {5 } =?
✅ Katsayıları bölüp katsayı olarak , kök içindekileri bölüp kök içine yazarız
20÷1\sqrt {40÷5}
🤓 Katsayısı olmayan kareköklü sayıların katsayısı 1 kabul edilir. 🤓
12\sqrt {8}
➡ 9\sqrt {28} ÷ 3\sqrt {7 } =?
✅ Katsayıları bölüp katsayı olarak , kök içindekileri bölüp kök içine yazarız
9÷3\sqrt {28÷7}
3\sqrt {4}
🤓 4 karekök dışına 2 olarak çıkar. 🤓
3×2=6
🤓 Karekökden çıkan sayı ile katsayı çarpılır. 🤓
Not: Kök içinde bulunan pay ve payda ayrı ayrı kök içinde yazılabilir.
✅ √a÷b = √a÷ √b
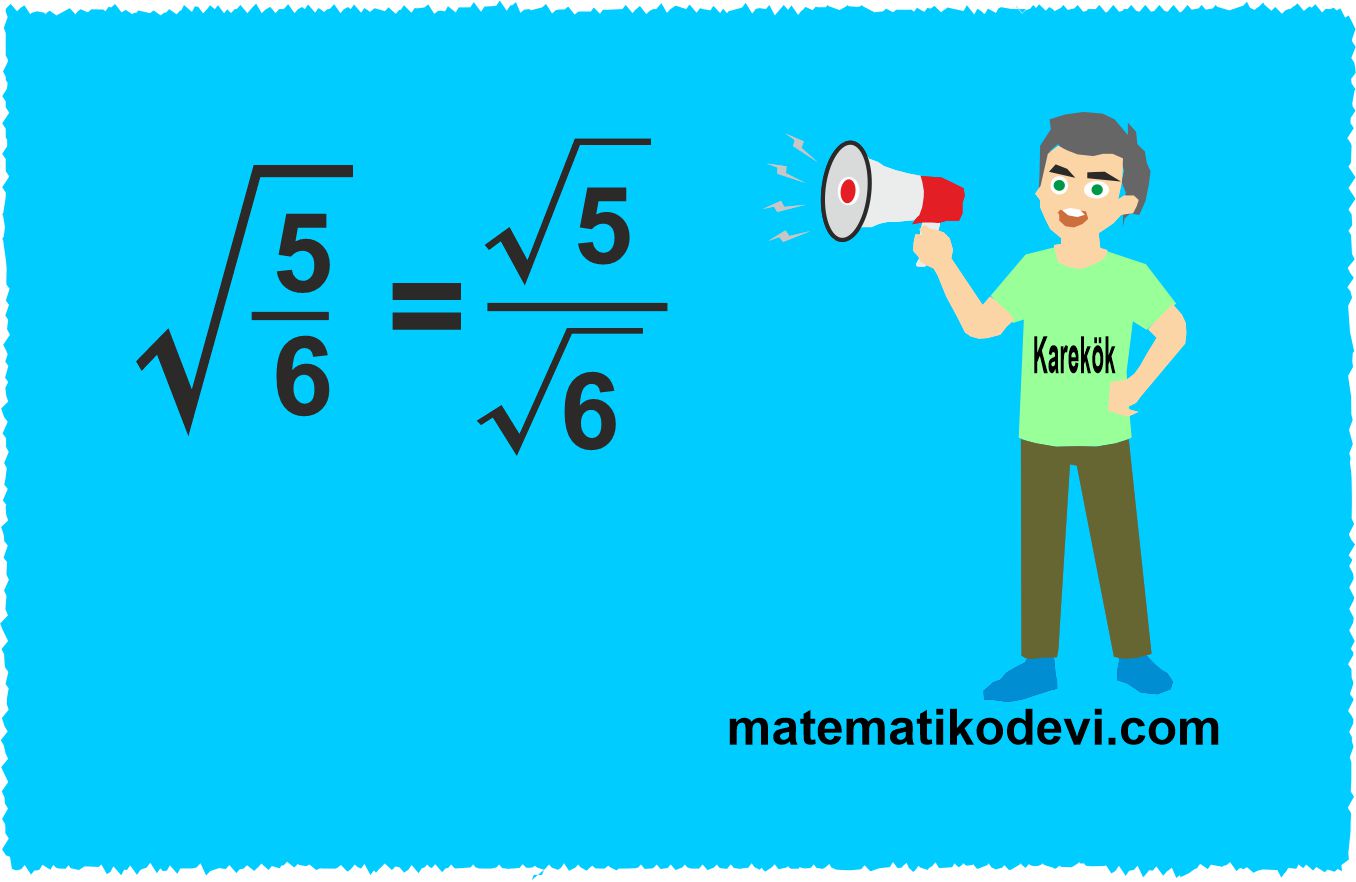
Not: Kareköklü bir sayının karesini aldığımızda (kendisiyle çarptığımızda) karekök işareti ortadan kalkar.
✅ √7× √7 = 7
✅ √8× √8 = 8
Örnek: Aşağıda bir kenar uzunluğu verilen karelerin alanını bulalım.
✅ 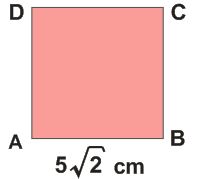
➡ Karenin alanı = 5\sqrt {2} × 5\sqrt {2}
➡ Katsayıların çarpalım.
5×5=25
➡ Kök içindekilerini çarpalım.
\sqrt {2} × \sqrt {2} = 2
➡ Katsayı ile kök içinden çıkan sayıyı çarpalım.
25×2=50
ABCD karesinin alanı 50 cm2 ‘dir.
✅ 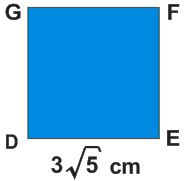
➡ Karenin alanını yazalım.
3\sqrt {5} × 3\sqrt {5}
➡ Katsayıların çarpalım.
3×3=9
➡ Kök içindekilerini çarpalım.
\sqrt {5} × \sqrt {5} = 5
➡ Katsayı ile kök içinden çıkan sayıyı çarpalım.
9×5=45
DEFG karesinin alanı 45 cm2 ‘dir.
Kareköklü Sayılarda Çarpma ve Bölme İşlemi Test
🎥 Bir Soru Bir Video 🎥
Soru:
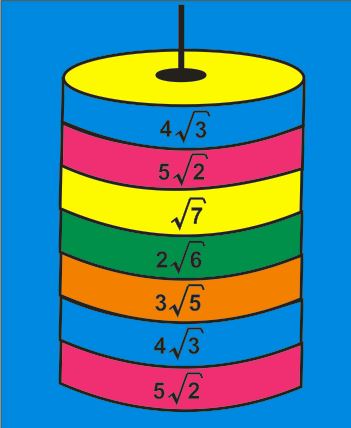
Üzerinde kareköklü sayılar yazılı olan 5 farklı renkteki diskler görseldeki gibi sırayla üst üste konularak 30 katlı yapı oluşturulmuştur. Bu yapı oluşturulurken 13.kattaki olması gereken disk unutulup sonrasında diğer katlar sırasına göre devam etmiştir.
Buna göre bu yapıdaki 25.kat ve 26.kattaki diskin üzerinde yazan kareköklü sayının çarpımı kaçtır?
| A) 12\sqrt {15} | B) 20\sqrt {6} | C) 6\sqrt {30} | D) 5\sqrt {14} |
Çözüm:

