Bölme İşlemi İle Kesir Arasındaki İlişki Konu Anlatımı
Kazanım: Bölme işlemi ile kesir kavramını ilişkilendirir.
Bu konuda neler öğreneceğiz :
Bölme İşlemi ile Kesir Arasındaki İlişki
Bölme işlemi ile kesir arasındaki ilişkiyi bir örnek ile açıklayalım.
🤔 2’yi 5’e nasıl böleriz❓
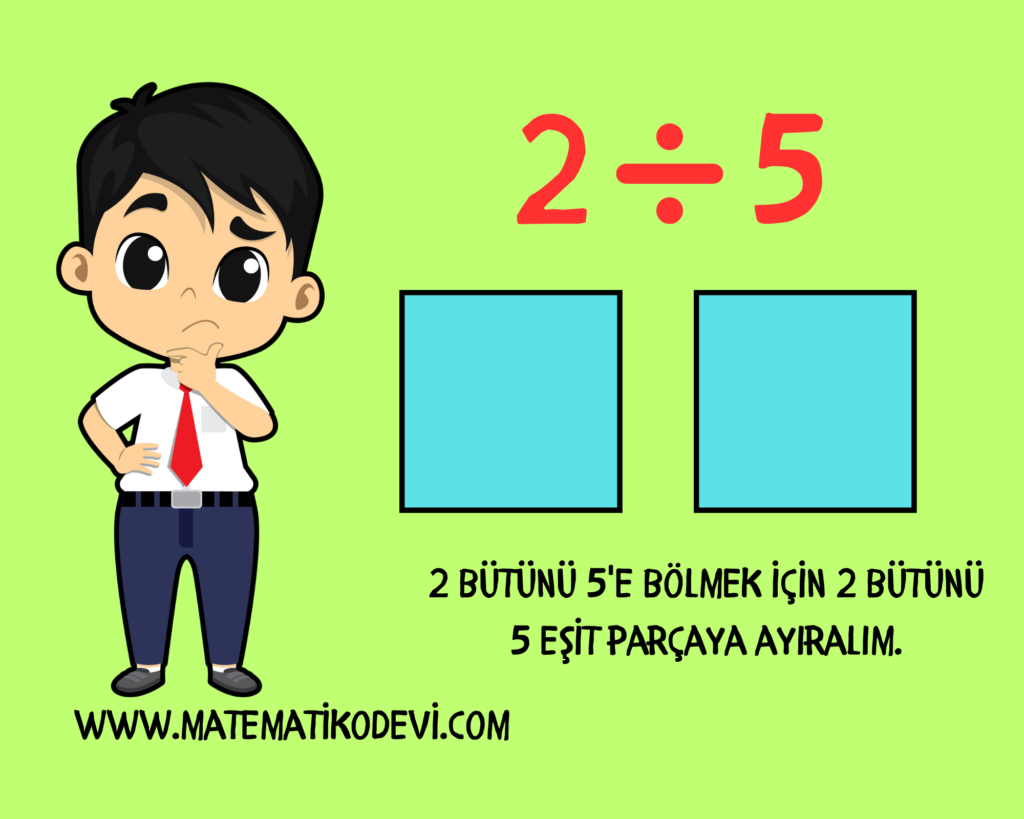
2 bütünü 5’e direk bölemeyiz. Bunun için her bütünü 5 eşit parçaya ayırmalıyız.
Her bütünü 5 eşit parçaya ayırdığımızda toplam 10 parça yapar. 10 parçayı 5’e böldüğümüzde 2 yapar.
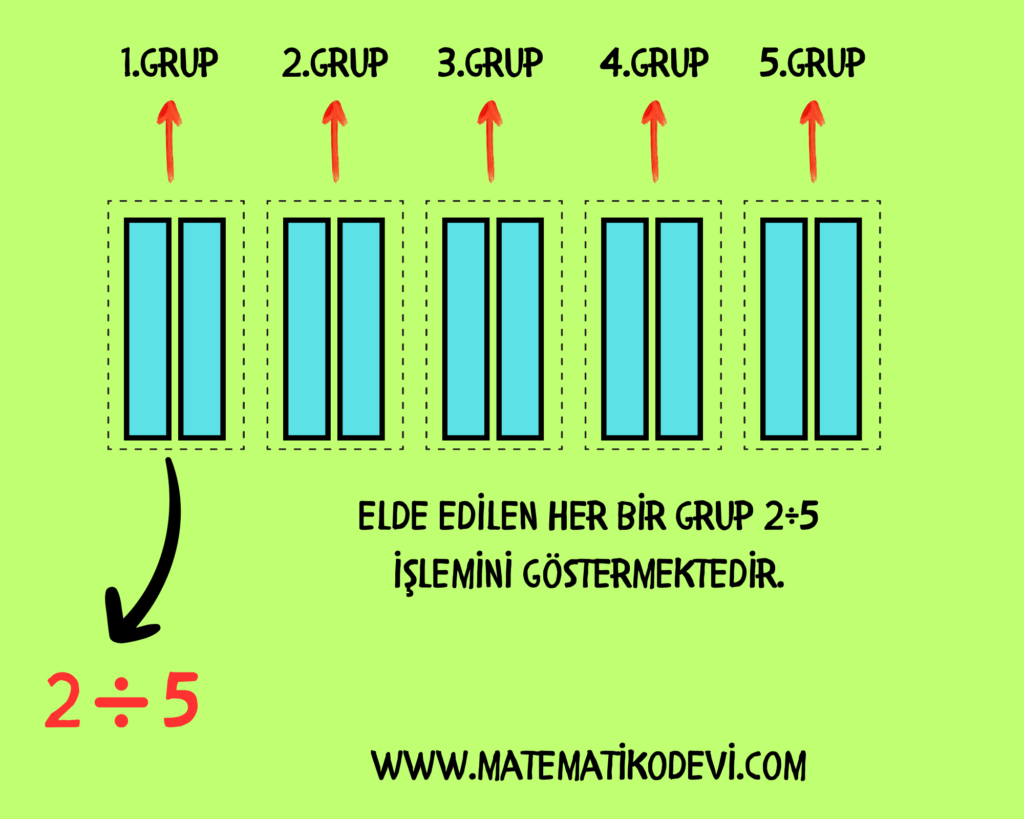
Sonuç olarak 2 bütünü 5’e böldük ve 2 parça elde ettik. Yani 5 parçadan 2 parça oldu. Bu durumu 5’te 2 olarak ifade ederiz. 5’te 2’yi ➡️ 2÷5 veya \dfrac{2}{5} olarak ifade ederiz.
2➗5 ➡️ 5’te 2 ➡️ \dfrac{2}{5}
Kesir şeklinde yazılan bir sayı, payın paydaya bölünmesi ile aynı anlama gelir.
✅ 2÷5 = \dfrac{2}{5}
✅ 7÷4 = \dfrac{7}{4}
✅ 3÷4 = \dfrac{3}{4}
Bölme İşlemi Yaparak Kesirleri Ondalık Gösterime Çevirme
Kesir şeklinde yazılan bir sayı, payın paydaya bölünmesi anlamına geldiğine göre bölme işlemi yaparak da bir kesri ondalık gösterime çevirebiliriz. Şimdi bir örnek ile açıklayalım.
Örneğin; \dfrac{8}{5} kesrinin ondalık gösterimini payını paydasına bölerek bulalım.

8’i 5’e böldüğümüzde 1 kere vardır. 8’den 5’içıkardığımızda 3 kalanını verir. Buradan sonrası 3’ün içinde 5 yok 3’ü 5’e bölebilmek için bölümdeki 1’in yanına virgül koyup 3’ün yanına sıfır atarız. Bu şekilde 30’u 5’e bölerek sonucu bulmuş oluruz.
Kesri ondalık gösterime çevirirken kesrin paydasını 10’un kuvveti olacak şekilde sadeleştirerek veya genişleterek ondalık olarak ifade edebiliriz.
Örneğin; Örneğin; \dfrac{8}{5} kesrinin ondalık gösterimini paydayı 10’un kuvveti yaparak bulalım.
🤔 Paydayı 2 ile genişletelim.
\dfrac{8·2}{5·2}
\dfrac{16}{10}
🤔 Tam kısımlı kesre dönüştürelim.
1 \dfrac{6}{10} = 1,6
Devirli Ondalık Gösterim
Bazı bölme işlemi
Bir ondalık gösterimde ondalık kısımda yer alan aynı rakam veya sayılar sonsuza kadar tekrar ediyorsa bu ondalık gösterime devirli ondalık gösterim denir.
Örneğin;
3,444444444444…………….. ➡️ Ondalık gösteriminde 4 rakamı sonsuza kadar tekrar ediyor. Bu yüzden bu ondalık gösterime devirli ondalık gösterim denir.
5,34242424242…………….. ➡️ Ondalık gösteriminde 42 sayısı sonsuza kadar tekrar ediyor. Bu yüzden bu ondalık gösterime devirli ondalık gösterim denir.
Ondalık gösterimde sürekli olarak tekrar eden basamak ya da basamaklar bir kez yazılır ve tekrar eden kısmın üzerine bir çizgi konularak gösterilir
Örneğin;
3,444444444444…………….. ➡️ 3, \overline{4}
5,34242424242…………….. ➡️ 5,3 \overline{42}

Bölme İşlemi İle Kesir Kavramını İlişkilendirme Test
🔻 Diğer konulara hızlı geçiş 🚀
| ⏪ Önceki Konu | Sonraki Konu ⏩ |
| Ondalık Gösterimleri Çözümleme Ve Yuvarlama |

